跑道式回旋加速器的工作原理如图所示。两个匀强磁场区域Ⅰ、Ⅱ的边界平行，相距为$L$，磁感应强度大小均为$B$，方向垂直纸面向里。$P$、$Q$之间存在匀强加速电场，电场强度为$E$，方向与磁场边界垂直。质量为$m$、电荷量为$+q$的粒子从$P$飘入电场，多次经过电场加速和磁场偏转后，从位于边界上的出射口$K$引出时动能为${{E}_{\text{k}}}$。已知$K$、$Q$的距离为$d$，带电粒子的重力不计。则下列说法正确的是$(\qquad)$

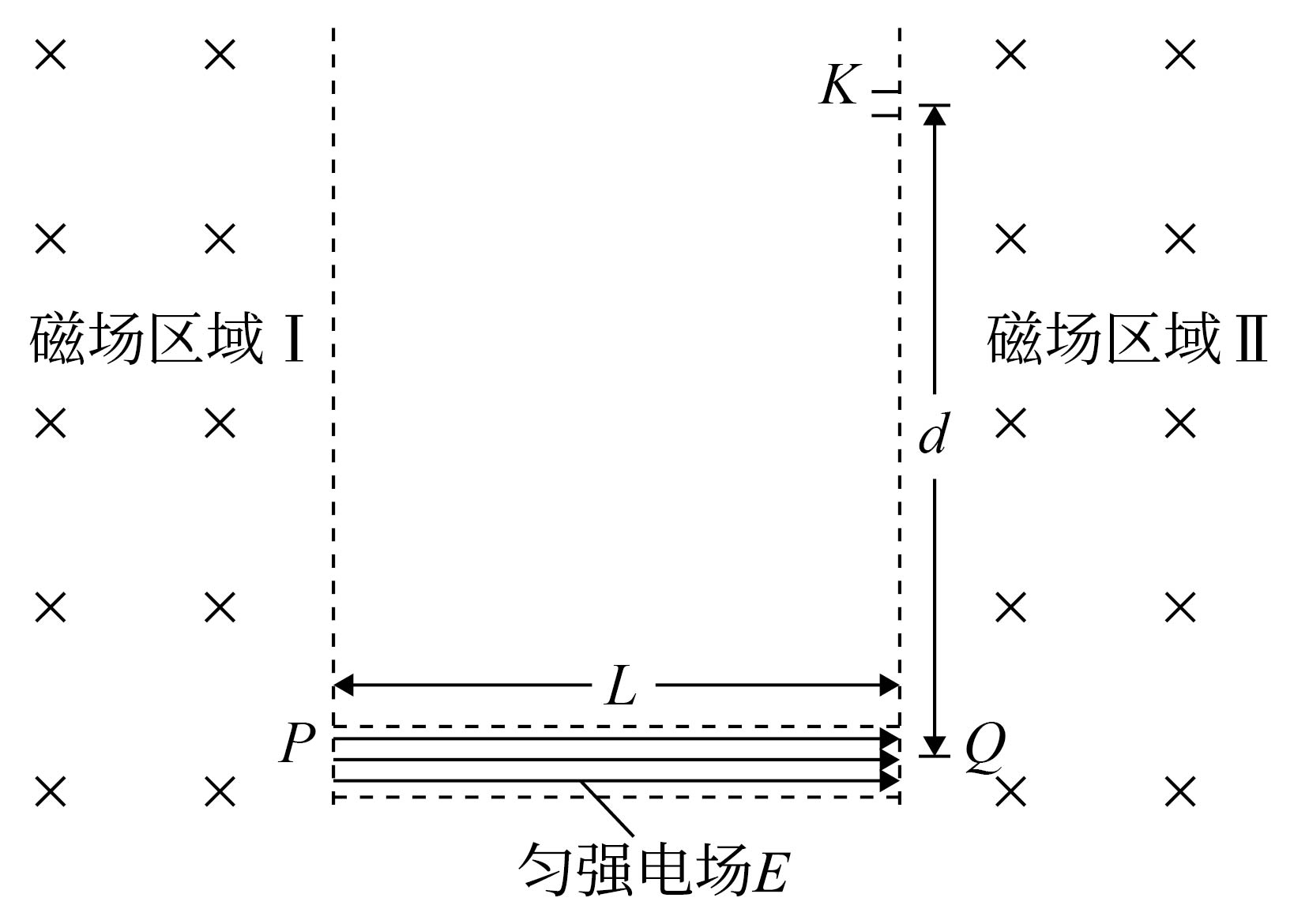
第一次加速后，粒子在Ⅱ中运动的半径比在Ⅰ中的半径大

粒子每次从$P$点被加速到再次回到$P$点所用的时间相同

粒子从出射口$K$引出的动能${{E}_{\\text{k}}}=\\dfrac{{{q}^{2}}{{B}^{2}}{{d}^{2}}}{8m}$

粒子出射前经过加速电场的次数$N=\\dfrac{q{{B}^{2}}{{d}^{2}}}{mEL}$

$\text{A}$、第一次加速后，粒子在Ⅱ中和在Ⅰ中的运动速率相等，由$r=\dfrac{mv}{qB}$分析可知，粒子在Ⅱ中运动的半径与在Ⅰ中的半径相等，故$\text{A}$错误；

$\text{B}$、粒子每次从$P$点被加速到再次回到$P$点在磁场中所用的时间相等，但在电场中所用时间不等，因为在电场中的平均速度不断增大，所用时间越来越短，所以粒子每次从$P$点被加速到再次回到$P$点所用的时间越来越短，故$\text{B}$错误；

$\text{C}$、设粒子从出射口$K$射出时的速度大小为${{v}_{\text{m}}}$，此时粒子在磁场中做匀速圆周运动的轨道半径最大，为$r=\dfrac{d}{2}$，粒子在磁场中做匀速圆周运动，由洛伦兹力提供向心力，由牛顿第二定律得：$q{{v}_{\text{m}}}B=m\dfrac{v_{\text{m}}^{2}}{r}$，粒子从出射口$K$射出时的动能${{E}_{\text{k}}}=\dfrac{1}{2}mv_{\text{m}}^{2}$，联立解得：${{E}_{\text{k}}}=\dfrac{{{q}^{2}}{{B}^{2}}{{d}^{2}}}{8m}$，故$\text{C}$正确；

$\text{D}$、设粒子在电场中加速次数是$N$，粒子在电场中加速过程，由动能定理得：${{E}_{\text{k}}}=NqEL$，解得：$N=\dfrac{q{{B}^{2}}{{d}^{2}}}{8mEL}$，故$\text{D}$错误。

故选：$\text{C}$。