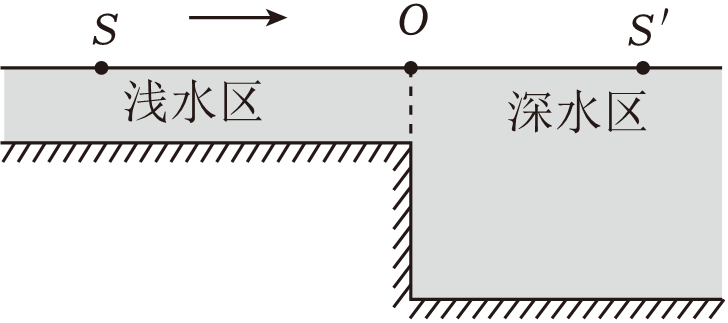
如图所示，某一宽阔水域由浅水区和深水区组成。浅水区水面$S$处有一波源由平衡位置开始沿竖直方向做简谐振动，起振方向向下，频率$f=2\;\rm Hz$，其向四周传播的水面波可近似看作简谐横波。波源产生的其中一列水面波沿直线$SOS$'传播，$O$点在浅水区和深水区的分界线上，$\overline{SO} = 9\;\rm m,\overline{OS'} = 7\;\rm m$，水面波在浅水区和深水区的传播速度之比为$3:4$。某时刻，该水面波正好传到$S$'处，且此时$O$、$S$均在波峰位置。已知该深水区的水面波波长在$\dfrac{2}{5}\;\rm m\sim \dfrac{1}{2}\;\rm m$范围内，则$(\qquad)$

$S$'的起振方向向下

该水面波在浅水区和深水区的波长之比为$4:3$

该浅水区的水面波波长为$\\dfrac{1}{3}\\;\\rm m$

该深水区的水面波波速为$\\dfrac{8}{9}\\;\\rm m/s$

$\rm A$、$S$'的起振方向与振源的起振方向相同应向下，故$\rm A$正确；

$\rm B$、波的周期不变，与介质无关，$\lambda=vT$，波长与波速成正比，所以波长之比为$3:4$，故$\rm B$错误；

$\rm CD$、$O$、$S$均在波峰，故$9=N_{1}\lambda_{1}$（$N_{1}=1$，$2$，$3$，⋯⋯），因为水面波正好传到$S$'处，

故$7 = N_{2}\lambda_{2} + \dfrac{3}{4}\lambda_{2}(N_{2} = 0,1,2, \cdot \cdot \cdot \cdot \cdot \cdot )$，则$\lambda_{2} = \dfrac{7}{N_{2} + \dfrac{3}{4}}$，

由题意$\dfrac{2}{5} \leqslant \dfrac{7}{N_{2} + \dfrac{3}{4}} \leqslant \dfrac{1}{2},N_{2}$可取$14$、$15$、$16$，

由于$\lambda_{1}:\lambda_{2}=3:4$，

则联立通解$7\;\rm N_{1}=12\;\rm N_{2}+9$，代入$N_{2}=14$、$15$、$16$，

要使$N_{1}$为整数可得$N_{2}=15$，$N_{1}=27$，

代入上述波长表达式，可得$\lambda_{1} = \dfrac{1}{3}\;\rm m$，$\lambda_{2} = \dfrac{4}{9}\;\rm m$，$v_{1} = \dfrac{2}{3}\;\rm m/s$，$v_{2} = \dfrac{8}{9}\;\rm m/s$，故$\rm CD$正确；

故选：$\rm ACD$。