某同学先用多用电表的欧姆挡粗测金属丝电阻，把选择开关调到“$\times 1$”挡，测量时多用电表的示数如图甲所示，则该元件电阻为$R=$                （$\rm A.11\;\rm \Omega$，  $\rm B.110\;\rm \Omega$）；再用螺旋测微器测量金属丝的直径$d$，其示数如图乙所示，则 $d=$                $\;\rm mm$；

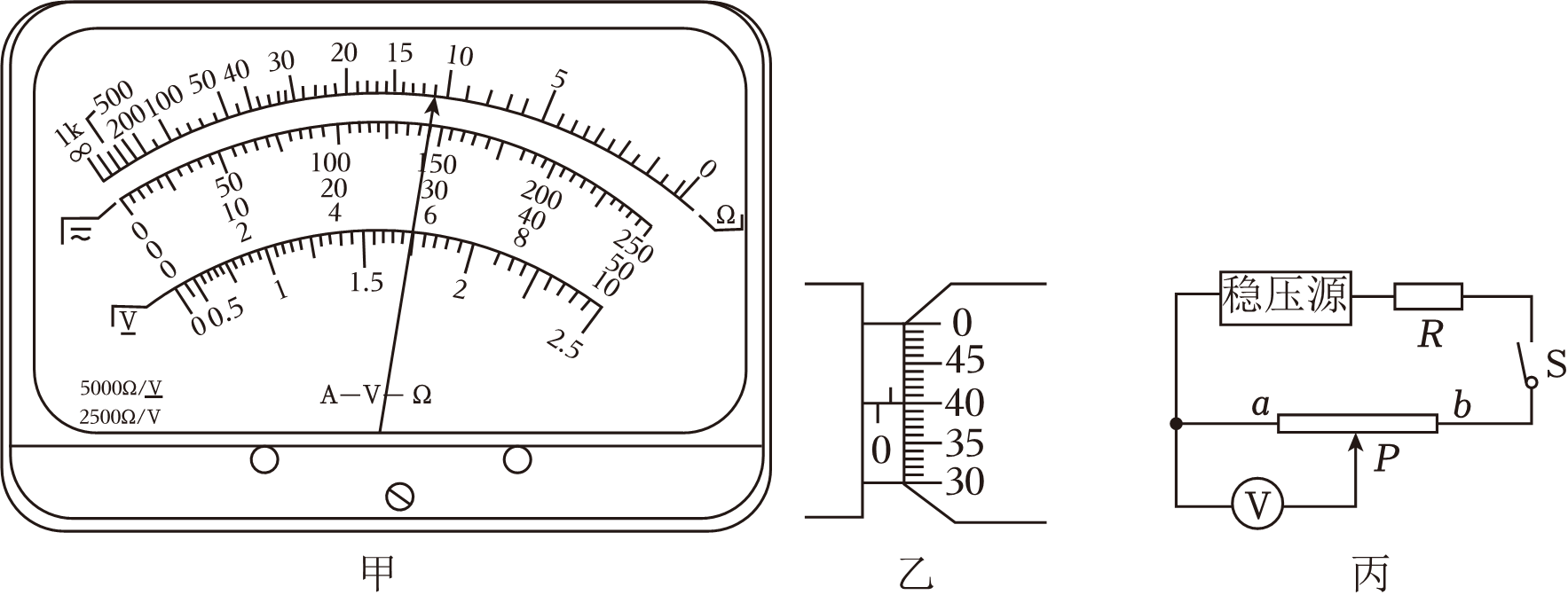
$\\rm A$；$0.900$

欧姆表测电阻，使用“$\times 1$”挡，待测电阻$R=11\times 1\;\rm \Omega=11\;\rm \Omega$，故$A$正确，$B$错误。

故选：$A$。

螺旋测微器的精确度为$0.01\;\rm mm$，金属丝直径$d=0.5\;\rm mm+40.0\times 0.01\;\rm mm=0.900\;\rm mm$。

为了精确测量金属丝电阻，小组成员甲同学根据实验室提供器材：滑动变阻器（阻值为$0\sim 15\;\rm \Omega$）、电流表（阻值约为$10\;\rm \Omega$）、电压表（阻值约为$3\;\rm k\Omega$），要求从零开始测量数据，请选择正确的电路图                ；

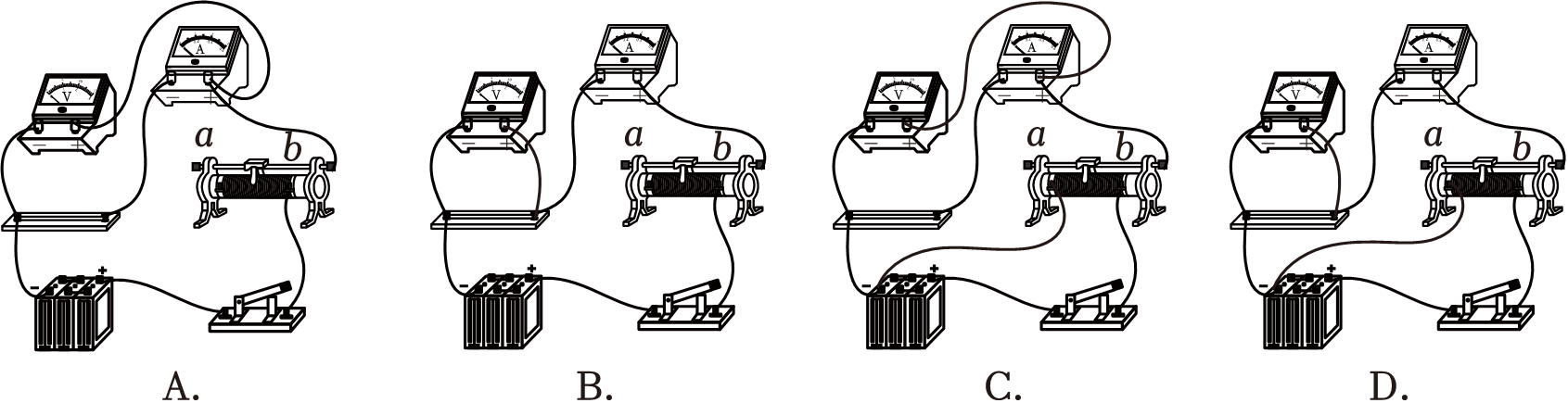
$\\rm D$

实验要求电压从零开始测量，因此滑动变阻器采用分压式接法；

由于$\dfrac{R_{x}}{R_{A}} = \dfrac{11}{10}\lt \dfrac{R_{V}}{R_{x}} = \dfrac{3000}{11}$，因此电流表采用外接法。

综上分析，故$\rm ABC$错误，$\rm D$正确。

故选：$\rm D$。

正确连接好第（$2$）问中的电路，某次实验时，电压表的示数为$U$，电流表的示数为$I$，测得金属丝的长为$L$，则金属丝电阻率$\rho=$                ；（用题中的符号$U$、$I$、$L$、$d$、$\pi$表示）

$\\dfrac{\\pi Ud^{2}}{4IL}$

根据欧姆定律，待测电阻$R = \dfrac{U}{I}$

根据电阻定律$R = \rho\dfrac{L}{S} = \dfrac{\rho L}{\dfrac{\pi d^{2}}{4}} = \dfrac{4\rho L}{\pi d^{2}}$

代入数据解得$\rho = \dfrac{\pi Ud^{2}}{4IL}$

小组成员乙同学设计了如图丙所示电路测量该金属丝电阻率，稳压源的输出电压恒为$U_{0}$，定值电阻的阻值为$R$，根据多次实验测出的$aP$长度$x$和对应的电压表的示数$U$作出的$U﹣x$图线，图线的斜率为$k$，则金属丝的电阻率$\rho=$                。（用题中的符号$k$、$R$、$d$、$U_{0}$、$L$表示）

$\\dfrac{k\\pi d^{2}R}{4(U_{0} - kL)}$

滑动变阻器的总电阻$R_{ab} = \dfrac{4\rho L}{\pi d^{2}}$

与电压表并联部分的电阻$R_{aP} = \dfrac{x}{L}R_{ab} = \dfrac{4\rho x}{\pi d^{2}}$

根据串联电路电压的分配与电阻的关系$\dfrac{U_{0}}{R + R_{ab}} = \dfrac{U}{R_{aP}}$

代入数据化简得$U = \dfrac{{4\rho U}_{0}}{\pi d^{2}R + 4\rho L} \cdot x$

结合$U﹣x$函数图像斜率的含义，图像斜率$k = \dfrac{4\rho U_{0}}{\pi d^{2}R + 4\rho L}$

解得电阻率$\rho = \dfrac{k\pi d^{2}R}{4(U_{0} - kL)}$。