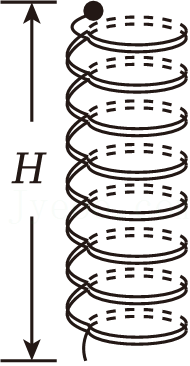
用长度为$L$的铁丝绕成一个高度为$H$的等螺距螺旋线圈，将它竖直地固定于水平桌面。穿在铁丝上的一小珠子可沿此螺旋线圈无摩擦地下滑（下滑过程线圈形状保持不变），已知重力加速度为$g$。这个小珠子从螺旋线圈最高点无初速滑到桌面经历的时间和速度分别为$(\qquad)$

$t = \\dfrac{L}{\\sqrt{2gH}}$

$v = \\sqrt{\\dfrac{gH}{2}}$

$t = L\\sqrt{\\dfrac{2}{gH}}$

$v = \\sqrt{2gH}$

将螺旋线圈分制为很多小段，每一段近似为一个斜面，由于螺旋线圈等螺距，说明每一小段的斜面倾角相同，设为$\theta$，根据几何关系，有$\sin\theta$$= \dfrac{H}{L}$，珠子做加速度大小恒定运动的加速，根据牛顿第二定律，有$mg\sin\theta=ma$，解得$a=g\sin\theta$$= \dfrac{Hg}{L}$，由于珠子与初速度和加速度大小相同的匀加速直线运动的运动时间完全相同，故根据位移$—$时间关系公式，有$L$$= \dfrac{1}{2}$$at^{2}$，联立解得$t=L$$\sqrt{\dfrac{2}{gH}}$，所以速度$v=at$$= \dfrac{Hg}{L}$$\cdot L$$\sqrt{\dfrac{2}{gH}} = \sqrt{2gH}$，故$\rm CD$正确，$\rm AB$错误。

故选：$\rm CD$。