高中 | 斜面问题 题目答案及解析
稿件来源:高途
高中 | 斜面问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
斜面问题
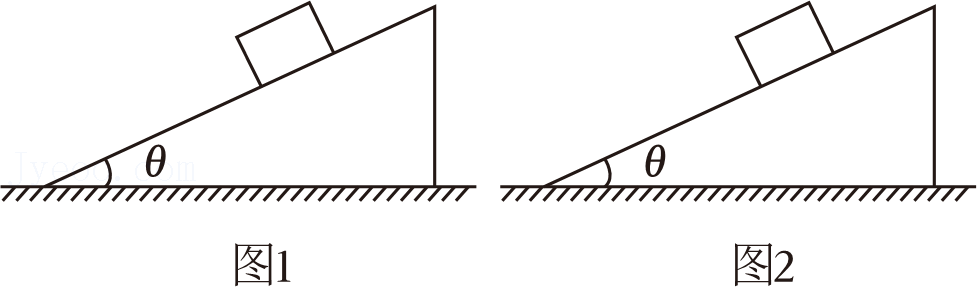
如图$1$:水平面上固定一个斜面,斜面光滑,斜面的倾角为$\theta$,斜面上有一个质量为$m$光滑木块,木块加速下滑,加速度平行于斜面,求木块的加速度的大小。
木块的加速度的大小为$g\\sin\\theta$
"]]根据牛顿第二定律,对木块分析有$mg\sin\theta=ma$,所以$a=g\sin\theta$
如图$2$:光滑的水平面上有一质量为$M$的楔子(即斜面),斜面的倾角为$\theta$,楔子没有固定在水平面上,楔子可以在水平面上左右滑动,楔子的斜面也光滑,楔子的斜面上有一质量为$m$的光滑木块。
①根据运动和空间想象力,判断木块下滑时,楔子是否也水平运动? (填写“是”或者“否”)。
②试求楔子的斜面对木块的斜向上的支持力。
③楔子是否有水平向右的加速度?如果有,请写出该加速度的表达式,如果没有,请说明理由。
①根据题意可知,木块下滑过程中,楔子给木块垂直斜面向上的作用力,由牛顿第三定律可知,木块给楔子斜向下的作用力,由于楔子不固定,且地面光滑,则楔子受力有水平向右的分力,则楔子会向右运动。
②以地面为参考系,楔子的加速度朝右,木块的相对于地面的加速度朝左(因为斜面对木块的支持力有水平分力),
设:木块的加速度水平向左的分加速度为$a_{1}$,竖直加速度为$a_{2}$,楔子水平向右的加速度大小为$a_{3}$,因为$a_{1}$和$a_{3}$反向,所以木块相对于楔子的水平向左的加速度为$a_{1}+a_{3}$。
以楔子为参考系,有$\dfrac{a_{2}}{a_{1} + a_{3}} = \tan\theta$,
设斜面对木块的斜向上的支持力为$N$,则$N$在水平方向的分力为$N\sin\theta$;$N$在竖直方向的分力为$N\cos\theta$;
$a_{1} = \dfrac{N\sin\theta}{m}$,$a_{3} = \dfrac{N\sin\theta}{M}$,$a_{2} = \dfrac{mg - N\cos\theta}{m}$,联立解得:$N = \dfrac{Mmg\cos\theta}{M + m\sin^{2}\theta}$
③由②可知,楔子是有水平向右的加速度,大小为$a_{3} = \dfrac{N\sin\theta}{M} = \dfrac{mg\sin\theta \cos\theta}{M + m\sin^{2}\theta}$
高中 | 斜面问题题目答案及解析(完整版)
