如图所示，一列简谐横波在$x$轴上传播，图甲和图乙分别为$x$轴上$a$、$b$两质点的振动图像，且$x_{ab}$为$6\;\rm m$。这列波的波长与波速可能的数值是$(\qquad)$

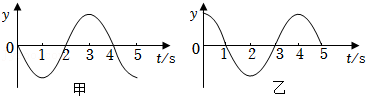
$\\lambda=24\\;\\rm m$

$\\lambda=8\\;\\rm m$

$v=1.2\\;\\rm m/s$

$v=0.2\\;\\rm m/s$

若波由$a$向$b$传播，因为在$0$时刻，质点$a$位于平衡位置向下振动，质点$b$位于波峰，那么有（$n+ \dfrac{1}{4})\lambda_{1}=x_{ab}(n=0.1.2$…），

则波长$\lambda_{1}= \dfrac{24}{4n + 1}\;\rm m$，又由$v_{1}= \dfrac{\lambda_{1}}{T}$解得:$v_{1}= \dfrac{6}{4n + 1}\;\rm m/s(n=0.1.2$…）

当$n=0$时$\lambda_{1}=24\;\rm m$、$v_{1}=6\;\rm m/s$

当$n=1$时，$\lambda_{1}=4.8\;\rm m$、$v_{1}=1.2\;\rm m/s$

若波由$b$向$a$传播，因为在$0$时刻，质点$a$位于平衡位置向下振动，质点$b$位于波峰，那么有（$n+ \dfrac{3}{4})\lambda_{2}=x_{ab}(n=0.1.2$…），

则波长$\lambda_{2}= \dfrac{24}{4n + 3}\;\rm m$，又由$v_{2}= \dfrac{\lambda_{2}}{T}$解得:$v_{2}= \dfrac{6}{4n + 3}\;\rm m/s(n=0.1.2$…）

当$n=0$时$\lambda_{2}=8\;\rm m$、$v_{2}=2\;\rm m/s$

当$n=1$时，$\lambda_{2}= \dfrac{24}{7}\;\rm m$、$v_{2}= \dfrac{6}{7}\;\rm m/s$，故$\rm ABC$正确、$\rm D$错误。

故选：$\rm ABC$。