| 动能定理解决多过程问题 题目答案及解析
稿件来源:高途
| 动能定理解决多过程问题题目答案及解析如下,仅供参考!
必修2
第七章 机械能守恒定律
7.7 动能和动能定理
动能定理解决多过程问题
如图所示,一半径$R=0.1\;\rm m$的光滑半圆形轨道$CD$与一粗糙水平轨道$BC$在$C$点平滑相连,$D$为轨道的最高点。光滑倾斜轨道$AB$与水平轨道$BC$在$B$点平滑连接。一小物块从距离水平面高度$h$的倾斜轨道上$A$点沿倾斜轨道自由滑下,经过水平轨道$BC$进入圆形轨道,沿着圆形轨道运动到最高点$D$,然后做平抛运动,落回水平轨道上$E$点,距$C$点的距离$s=0.2\;\rm m$。小物块与水平轨道间的动摩擦因数$\mu =0.1$,水平轨道$BC$的长度$x=3\;\rm m$,重力加速度$g=10\;\rm m/s^{2}$。求:
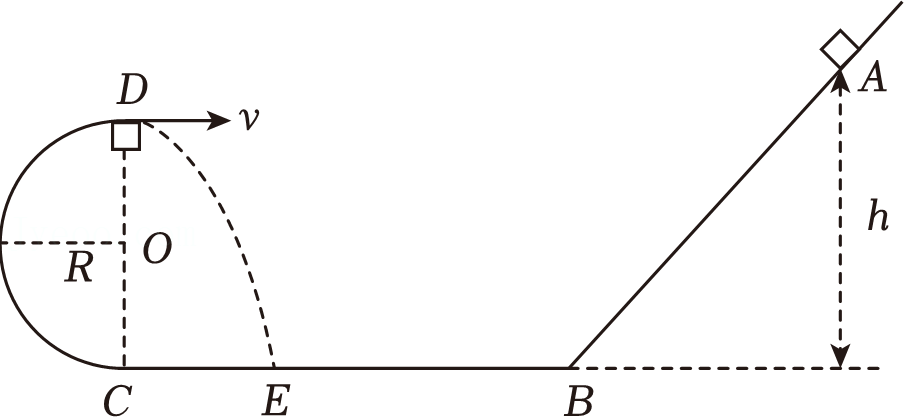
小物块在$D$点做平抛运动的速度;
[["
小物块在$D$点做平抛运动的速度为$1\\;\\rm m/s$
"]]根据平抛运动规律
竖直方向上$2R = \dfrac{1}{2}gt^{2}$
水平方向
$s=v_{D}t$
得
$v_{D}=1\;\rm m/s$
高度$h$。
[["
小物块从距离水平面高度为$0.55\\;\\rm m$
"]]对小物块从$A$到$D$的过程中,根据动能定理$mgh - 2mgR - \mu mgx = \dfrac{1}{2}mv_{D}^{2}$
得
$h=0.55\;\rm m$
| 动能定理解决多过程问题题目答案及解析(完整版)
去刷题
今日推荐 ![]()
![]()
![]()
