| 动能定理解决多过程问题 题目答案及解析
稿件来源:高途
| 动能定理解决多过程问题题目答案及解析如下,仅供参考!
必修2
第七章 机械能守恒定律
7.7 动能和动能定理
动能定理解决多过程问题
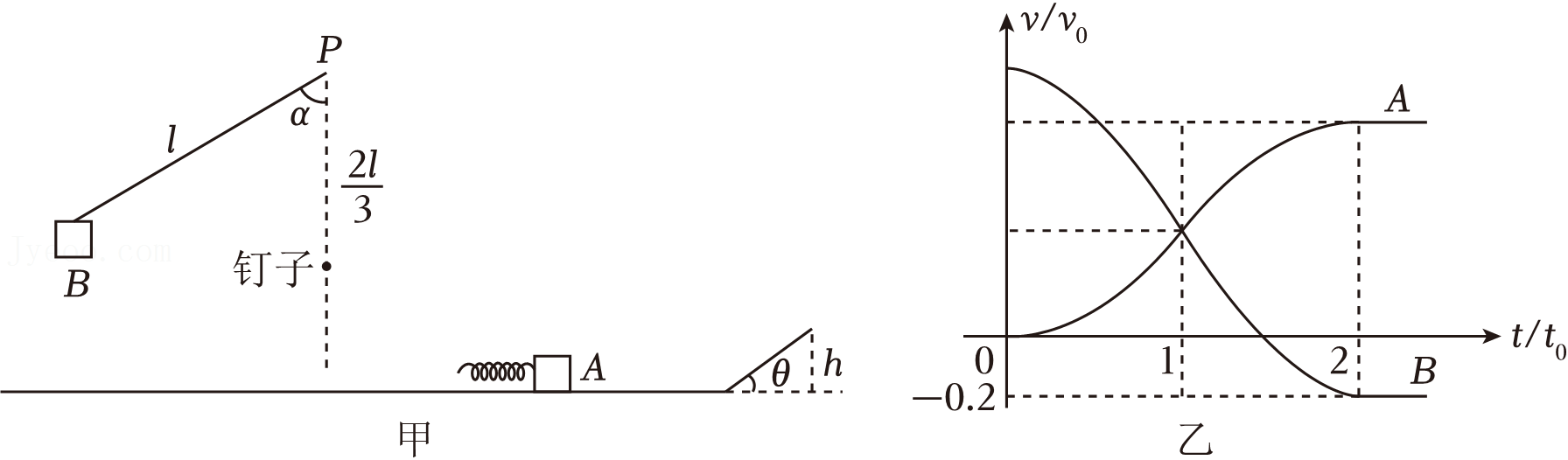
如图甲,一质量为$2m$的物块$B$用一长度为$l = \dfrac{v_{0}^{2}}{g}$的轻绳悬挂于$P$点处,初始时其与竖直方向的夹角$\alpha=60^\circ$,$P$点正下方$\dfrac{2l}{3}$处有一钉子。另一物块$A$与轻质弹簧连接,静止于光滑水平面上。现自由释放物块$B$,当其运动至$P$点正下方时轻绳在钉子的作用下断裂。之后物块$B$将在光滑水平面上匀速直线运动,直至与物块$A$发生碰撞(假定在物块$B$触地过程中机械能没有损失,轻绳在断裂后不影响物块$B$的后续运动)。记物块$B$第一次与弹簧接触的时刻为$t=0$,第一次与弹簧分离的时刻为$t=2t_{0}$。第一次碰撞过程中,$A$、$B$的$v-t$图像如图乙所示。已知从$t=0$到$t=t_{0}$时间内,物块$A$运动的距离为$0.144v_{0}t_{0}$。$A$、$B$分离后,$A$滑上粗糙斜面,然后滑下,与一直在水平面上运动的$B$再次碰撞。斜面倾角$\theta=37^\circ$,高度$h = \dfrac{v_{0}^{2}}{5g}$,与水平面光滑连接。已知碰撞过程中弹簧始终处于弹性限度内,重力加速度记为$g$,$\sin\theta=0.6$。求:
轻绳即将断裂时的张力;
轻绳即将断裂时的张力为$8mg$
"]]设$B$摆至最低点的速度为$v$,根据动能定理有:$2mgl(1-\cos\alpha)= \dfrac{1}{2} \times 2mv^{2}$
代入题设条件解得:$v=v_{0}$
设轻绳即将断裂时其中的张力为$F_{T}$,对$B$受力分析,根据牛顿第二定律有:$F_{T} - 2mg = 2m\dfrac{v^{2}}{l - \dfrac{2}{3}l}$
代入数据解得:$F_{T}=8mg$
第一次碰撞过程中,弹簧压缩量的最大值(用$v_{0}$、$t_{0}$表示);
第一次碰撞过程中,弹簧压缩量的最大值为$0.64v_{0}t_{0}$
"]]设$A$的质量为$m_{A}$,碰后$A$的速度为$v_{A}$,$B$与$A$发生完全弹性正碰,碰撞前后动量守恒,
以向右为正有:$2mv_{0}=m_{A}v_{A}+2m\cdot (-0.2v_{0}$ )
机械能守恒:$\dfrac{1}{2} \times 2mv_{0}^{2} = \dfrac{1}{2}m_{A}v_{A}^{2} + \dfrac{1}{2} \times 2m(0.2v_{0})^{2}$
解得:$m_{A}=3m$,$v_{A}=0.8v_{0}$
易知$t=t_{0}$时弹簧压缩量最大,记为$\Delta x$。设压缩过程中$A$的速度为$v_{A}(t)$,$B$,$B$的速度为$v_{B}(t)$
微分求和得:$\Delta x = \sum_{t = 0}^{t_{0}}\ v_{B}(t)\Delta t - \sum_{t = 0}^{t_{0}}\ v_{A}(t)\Delta t$
利用动量守恒:$3mv_{A}+2mv_{B}=2mv_{0}$
将$v_{B}(t)$用$v_{A}(t)$,$B$替换可得:$\Delta x = v_{0}t_{0} - \dfrac{5}{2}\sum_{t = 0}^{t_{0}}\ v_{A}(t)\Delta t$
代入题给条件:$\sum_{t = 0}^{t_{0}}\ v_{A}(t)\Delta t = 0.144v_{0}t_{0}$
可求得:$\Delta x=0.64v_{0}t_{0}$
物块$A$与斜面间的动摩擦因数$\mu $的取值范围。
物块$A$与斜面间的动摩擦因数$\\mu $的取值范围为$\\dfrac{9}{20} \\leqslant \\mu \\lt \\dfrac{45}{68}$
"]]$A$若要与$B$发生二次碰撞,其不能越过斜面。设$A$在斜面顶端的速度为$v_{m}$,由动能定理得$- 3mgh - 3\mu mg\cos\theta \cdot \dfrac{h}{\sin\theta} = \dfrac{1}{2} \times 3mv_{m}^{2} - \dfrac{1}{2} \times 3m(0.8v_{0})^{2}$
不能越过斜面即等价于:$v_{m}^{2} \leqslant 0$
代入可解得:$\mu \geqslant \dfrac{9}{20}$
$A$若要与$B$发生二次碰撞,其除了不能越过斜面之外,其返回至水平面时速度大小必须比$B$的大。设此时$A$在斜面上的最大高度为$h_{m}$,返回水平面时的速度为$v^\prime$,根据动能定理得$- 3mgh_{m} - 3\mu mg \cdot \dfrac{h_{m}}{\tan\theta} = - \dfrac{1}{2} \times 3m(0.8v_{0})^{2}$
$3mgh_{m} - 3\mu mg \cdot \dfrac{h_{m}}{\tan\theta} = \dfrac{1}{2} \times 3m(v')^{2}$
从中可以得到$v^\prime$与$v_{0}$的关系:($v^\prime)^{2}= \dfrac{16(\tan\theta - \mu)}{25(\tan\theta + \mu)}v_{0}^{2}$
$A$返回的速度$v^\prime$要大于$B$在水平面上的速度$0.2v_{0}$,代入可解得:$\mu \lt \dfrac{45}{68}$
最后,$A$能够从斜面上滑下必须满足条件:$3mg\sin\theta-3\mu mg\cos\theta\geqslant 0$
从中解得:$\mu \leqslant \dfrac{3}{4}$
综上可得$A$与斜面间的动摩擦因数应满足:$\dfrac{9}{20} \leqslant \mu \lt \dfrac{45}{68}$
| 动能定理解决多过程问题题目答案及解析(完整版)
