| 动量守恒之木板滑块模型 题目答案及解析
稿件来源:高途
| 动量守恒之木板滑块模型题目答案及解析如下,仅供参考!
选修3-5
第十六章 动量守恒定律
16.3 动量守恒定律
动量守恒之木板滑块模型
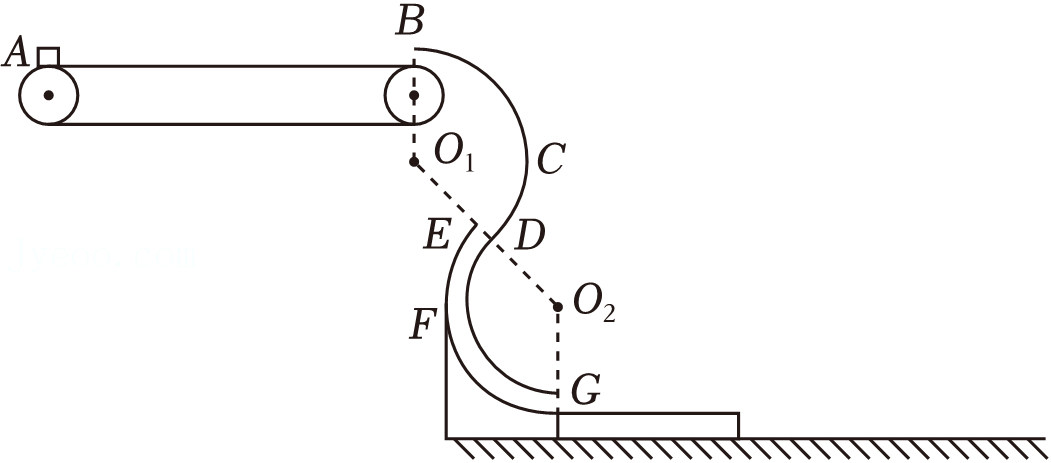
如图所示为一处于竖直平面内的实验探究装置的示意图,该装置由速度可调的固定水平传送带、光滑圆弧轨道$BCD$和光滑细圆管$EFG$组成,其中水平传送带长$L_{1}=3\;\rm m$,$B$点在传送带右端转轴的正上方,轨道$BCD$和细圆管$EFG$的圆心分别为$O_{1}$和$O_{2}$、圆心角均为$\theta=120^\circ$、半径均为$R=0.4\;\rm m$,且$B$点和$G$点分别为两轨道的最高点和最低点。在细圆管$EFG$的右侧足够长的光滑水平地面上紧挨着一块与管口下端等高、长$L_{2}=2.2\;\rm m$、质量$M=0.4\;\rm kg$木板(与轨道不粘连)。现将一块质量$m=0.2\;\rm kg$的物块(可视为质点)轻放在传送带的最左端$A$点,由传送带自左向右传动,在$B$处的开口和 $E$、$D$处的开口正好可容物块通过。已知物块与传送带之间的动摩擦因数$\mu _{1}=0.2$,物块与木板之间的动摩擦因数$\mu _{2}=0.5$,重力加速度$g=10\;\rm m/s^{2}$。
若物块进入圆弧轨道$BCD$后恰好不脱轨,求物块在传送带上运动的时间;
物块在传送带上运动的时间为$2\\;\\rm s$
"]]若物块进入圆弧轨道$BCD$后恰好不脱轨,则在$B$点有$mg= \dfrac{mv_{B}^{2}}{R}$
可得$v_{B}=2\;\rm m/s$
物体在传送带上运动时,由$\mu _{1}mg=ma$
可得$a=2\;\rm m/s^{2}$
若物块一直加速,则末速度为$v= \sqrt{2aL_{1}}$,解得$v=2\sqrt{3}\rm m/s\gt v_{B}$
由此可知物块应该是先加速后匀速,则加速的位移$x= \dfrac{v_{B}^{2}}{2a}$,解得$x=1\;\rm m$
物块在传送带上运动的时间$t= \dfrac{v_{B}}{a} + \dfrac{L_{1} - x}{v_{B}}$,解得$t=2\;\rm s$
若传送带的速度为$3\;\rm m/s$,求物块经过圆弧轨道$EFG$最低点$G$时,轨道对物块的作用力大小;
轨道对物块的作用力大小为$18.5\\;\\rm N$
"]]若传送带的速度$3\;\rm m/s$,则物体先加速后匀速,经过$B$点时的速度为$3\;\rm m/s$,由动能定理可得$mg(R+2R\sin30^\circ+R)= \dfrac{1}{2}mv_{G}^{2} - \dfrac{1}{2}mv_{B1}^{2}$
由牛顿第二定律有$F_{N}-mg= \dfrac{mv_{G}^{2}}{R}$
联立可得轨道对物块的作用力大小$F_{N}=18.5\;\rm N$
若传送带的最大速度为$5\;\rm m/s$,在不脱轨的情况下,求滑块在木板上运动过程中产生的热量$Q$与传送带速度$v$之间的关系。
滑块在木板上运动过程中产生的热量传送带速度$v$之间的关系满足:当$2\\;\\rm m/s\\leqslant v\\leqslant 3\\;\\rm m/s$时,$Q= \\dfrac{24 + v^{2}}{15}\\;\\rm J$;当$3\\;\\rm m/s\\lt v\\leqslant 5\\;\\rm m/s$时,$Q=2.2\\;\\rm J$
"]]若在木板上恰好不分离,设物块在$B$的速度为$v_{B2}$,在$G$点的速度为$v_{G1}$,物块与木板共速的速度为$v_{2}$,根据动量守恒有$mv_{G1}=(M+m)v_{2}$
根据动能定理有$\mu _{2}mgL_{2}= \dfrac{1}{2}mv_{G1}^{2} - \dfrac{1}{2}(M+m)v_{2}^{2}$
根据动能定理有$mg(R+2R\sin30^\circ+R)= \dfrac{1}{2}mv_{G1}^{2} - \dfrac{1}{2}mv_{B2}^{2}$
联立可得$v_{B2}=3\;\rm m/s$
则当$2\;\rm m/s\leqslant v\leqslant 3\;\rm m/s$时,有$Q= \dfrac{1}{2}mv_{G}^{2} - \dfrac{1}{2}(M+m)v_{2}^{2}$,得$Q= \dfrac{24 + v^{2}}{15}J$
则当$3\;\rm m/s\lt v\leqslant 5\;\rm m/s$时,有$Q=\mu _{2}mgL_{2}$,解得$Q=2.2\;\rm J$
| 动量守恒之木板滑块模型题目答案及解析(完整版)
