| 动能定理解决多过程问题 题目答案及解析
稿件来源:高途
| 动能定理解决多过程问题题目答案及解析如下,仅供参考!
必修2
第七章 机械能守恒定律
7.7 动能和动能定理
动能定理解决多过程问题
如图所示,$ABCD$是一个盆式容器,盆内侧与盆底$BC$的连接处都是一段与$BC$相切的圆弧。$BC$水平,其长度$d=0.50m$,盆边缘的高度$h=0.20m$.在$A$处放一个质量为$m=1\;\rm kg$的小物块并让其自由下滑。已知盆内侧壁是光滑的,而盆底$BC$面与小物块间的动摩擦因数$\mu =0.10$,小物块在盆内来回滑动,最后停下来,$g=10\;\rm m/s^{2}$。求:
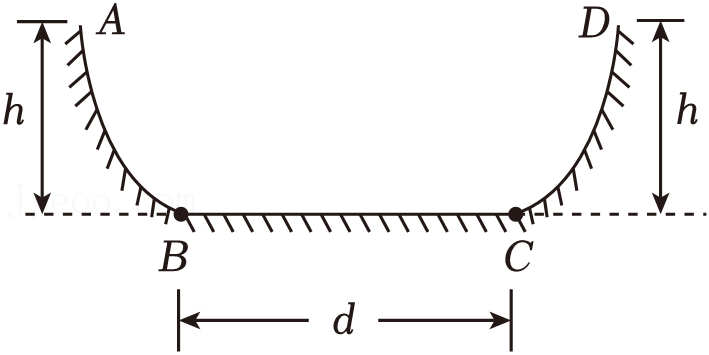
小物块第一次滑到$C$点时的动能$E_{k}$。
[["
小物块第一次滑到$C$点时的动能$E_{k}$为$1.5\\;\\rm J$
"]]依题意,小物块第一次滑到$C$点时的动能为$E_{k}$,
根据动能定理有$E_{k}=mgh﹣\mu mgd=1\times 10\times 0.2\;\rm J﹣0.1\times 1\times 10\times 0.5\;\rm J=1.5\;\rm J$
小物块最终停下的地点到$B$的距离$l$。
[["
小物块最终停下的地点到$B$的距离$l$为$0$
"]]设小物块在盆底滑行的路程为$s$,根据动能定理有$mgh﹣\mu mgs=0$
代入数据解得$s=2\;\rm m$
可知小物块在盆底刚好经过两个来回,最终停在$B$点,故$l=0$
| 动能定理解决多过程问题题目答案及解析(完整版)
去刷题
今日推荐 ![]()
![]()
![]()
