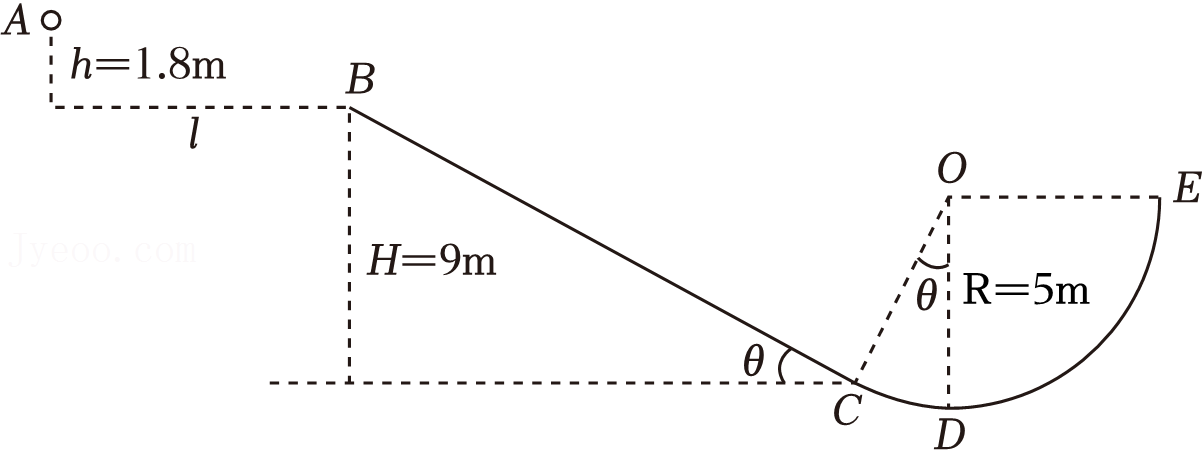
运动员到达$B$点时的速度大小；

运动员到达$B$点时的速度大小为$10\\;\\rm m/s$

分解运动员到达$B$点的速度，有：$v_{B}= \dfrac{v_{By}}{\sin 37{^\circ}}$

竖直方向根据速度$—$位移公式有：$v_{By} = \sqrt{2gh}$

联立代入数据解得：$v_{B}=10\;\rm m/s$

第一次到达$D$点时滑板对$D$点的压力；

第一次到达$D$点时滑板对$D$点的压力为$3480\\;\\rm N$，方向竖直向下

运动员从$B$运动到$D$，由动能定理有：$mgH - \mu mg\dfrac{H}{\sin\theta}\cos\theta + mgR(1 - \cos\theta) = \dfrac{1}{2}mv_{D}^{2} - \dfrac{1}{2}mv_{B}^{2}$

运动员在$D$点，受力分析根据牛顿第二定律可得$F_{N} - mg = \dfrac{mv_{D}^{2}}{R}$

联立代入数据解得：$F_{N}=3480\;\rm N$

根据牛顿第三定律可知$F_{压}=F_{N}=3480\;\rm N$，方向竖直向下

运动员有几次向上冲出$E$点的机会。

运动员有$2$次向上冲出$E$点的机会

要冲出$E$点，在$C$点的速度$v_{c}$必须满足：$\dfrac{1}{2}mv_{C\min}^{2} = mgR\cos\theta$

解得：$v_{C\min}^{2} = 80\;\rm m^{2}/s^{2}$

由牛顿第二定律有：$mg\sin\theta-\mu mg\cos\theta=ma_{1}$

代入数据解得：$a_{1} = 4\;\rm m/s^{2}$

根据运动学公式：$v_{C1}^{2} − v_{B}^{2}=2a_{1}\dfrac{H}{\sin\theta}$

代入数据解得：$v_{C1}^{2} = 220\;\rm m^{2}/s^{2}$

$v_{C1}^{2}\gt v_{C\min}^{2}$第一次能冲出$E$点

返回时，由牛顿第二定律有：$mg\sin\theta+\mu mg\cos\theta=ma_{2}a_{2} = 8\;\rm m/s^{2}$

$x = \dfrac{v_{c1}^{2}}{2a_{2}}$

代入数据解得：$x=13.75\text m\lt 15\;\rm m$．

再次返回$C$点的速度：$v_{c2}^{2} = 2a_{1}x$

代入数据解得：$v_{C2}^{2}=110\;\rm m^{2}/s^{2}$

$v_{c2}^{2}\gt v_{C\min}^{2}$，第二次能冲出$E$点，再次返回$v_{c3}^{2} = \dfrac{a_{1}}{a_{2}}v_{c2}^{2}$

代入数据解得：$v_{C3}^{2} = 55\;\rm{m^{2}/s^{2}}\lt v_{C\min}^{2}$

第三次不能冲上$E$点，综上所述总共能有$2$次冲上$E$点的机会