| 动量守恒之木板滑块模型 题目答案及解析
稿件来源:高途
| 动量守恒之木板滑块模型题目答案及解析如下,仅供参考!
选修3-5
第十六章 动量守恒定律
16.3 动量守恒定律
动量守恒之木板滑块模型
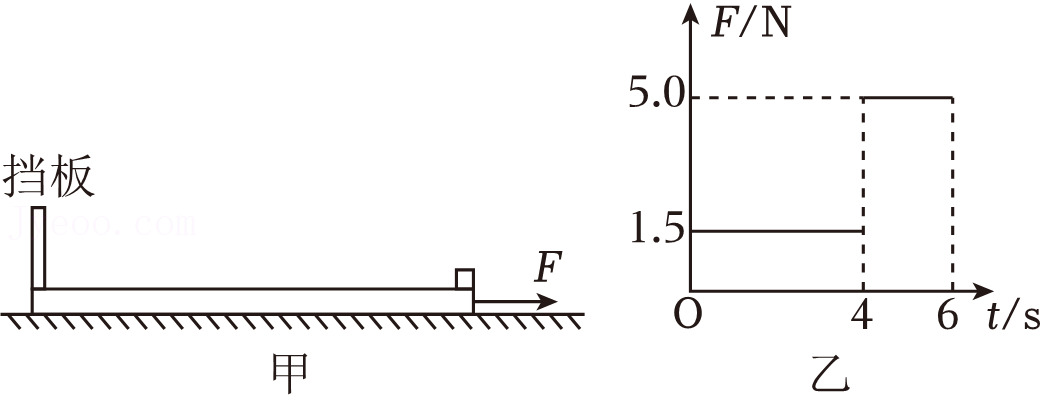
某物流公司研发团队,为了更好地提高包裹的分收效率,特对包裹和运输装置进行详细的探究,其情景可以简化为如图甲所示,质量$M=2\;\rm kg$、长度$L=2\;\rm m$的长木板静止在足够长的水平面(可视为光滑)上,左端固定一竖直薄挡板,右端静置一质量$m=1\;\rm kg$的包裹(可视为质点)。现机器人对长木板施加一水平向右的作用力$F$,$F$随时间$t$变化的规律如图乙所示,$6\;\rm s$后将力$F$撤去。已知包裹与挡板发生弹性碰撞且碰撞时间极短,包裹与长木板间的动摩擦因数$\mu =0.1$,重力加速度取$g=10\;\rm m/s^{2}$。从施加作用力$F$开始计时,求:
$t_{1}=4\;\rm s$时,长木板的速度$v_{1}$大小;
$t_{1}=4\\;\\rm s$时,长木板的速度$v_{1}$大小为$2\\;\\rm m/s$
"]]包裹与长木板刚要发生相对滑动时,对包裹有
$\mu mg=ma_{0}$
对包裹与长木板整体有:$F=(M+m)a_{0}$
联立得包裹与长木板发生相对滑动的力的大小为:$F=\mu (M+m)g=0.1\times (2+1)\times 10\;\rm N=3\;\rm N$
因为$1.5\;\rm N\lt 3\;\rm N$,所以$0-4\;\rm s$内,包裹和长木板会共同加速,加速度为$a = \dfrac{1.5}{1 + 2}\;\rm m/s^{2} = 0.5\;\rm m/s^{2}$
可得到:$v_{1}=at=0.5\times 4\;\rm m/s=2\;\rm m/s$
与挡板碰撞后瞬间,包裹的速度$v^\prime_{m}$大小;
与挡板碰撞后瞬间,包裹的速度$v^\\prime_{m}$大小为$\\dfrac{20}{3}m/s$
"]]假设$4\;\rm s$后包裹与长木板发生相对滑动,则包裹的加速度为
$a_{1}= \dfrac{\mu mg}{m} =\mu g=0.1\times 10\;\rm m/s^{2}=1\;\rm m/s^{2}$
长木板的加速度为
$a_{2}= \dfrac{F - \mu mg}{M} = \dfrac{5.0 - 0.1 \times 1 \times 10}{2}\;\rm m/s^{2}=2\;\rm m/s^{2}$
可看出假设成立,包裹与长木板发生相对滑动,设再经时间$t_{2}$包裹与挡板发生碰撞,由$L = (v_{1}t_{2} + \dfrac{1}{2}a_{2}t_{2}^{2}) - (v_{1}t_{2} + \dfrac{1}{2}a_{1}t_{2}^{2})$
解得:$t_{2}=2\;\rm s$
则$6\;\rm s$时长木板的速度:$v_{2}=v_{1}+a_{2}t_{2}=(2+2\times 2)\;\rm m/s=6\;\rm m/s$
包裹的速度为:$v_{3}=v_{1}+a_{1}t_{2}=(2+1\times 2)\;\rm m/s=4\;\rm m/s$
此时两者发生弹性碰撞,取向右为正方向,根据动量守恒定律和机械能守恒定律得
$mv_{3}+Mv_{2}=mv^\prime_{m}+Mv^\prime_{2}$
$\dfrac{1}{2}{mv}_{3}^{2} + \dfrac{1}{2}{Mv}_{2}^{2} = \dfrac{1}{2}mv{^\prime}_{m}^{2}+ \dfrac{1}{2}Mv{^\prime}_{2}^{2}$
可求得:$v'_{m} = \dfrac{20}{3}\;\rm m/s$
包裹最终离挡板的距离$d$。
包裹最终离挡板的距离$d$为$\\dfrac{4}{3}\\;\\rm m$
"]]最终离挡板的距离即两者共速的时候,取向右为正方向,根据动量守恒
$mv_{3}+Mv_{2}=(m+M)v_{共}$
根据能量守恒定律得
$\mu mgx= \dfrac{1}{2}{mv}_{3}^{2} + \dfrac{1}{2}{Mv}_{2}^{2} - \dfrac{1}{2}(m+M)v_{共}^{2}$
解得:$x = \dfrac{4}{3}\;\rm m$
由于$\dfrac{4}{3}\text m\lt 2\;\rm m$,故故包裹与长木板相对静止,故包裹离挡板距离$d = \dfrac{4}{3}\;\rm m$。
| 动量守恒之木板滑块模型题目答案及解析(完整版)
