对于矩形框的制作，甲同学选择了一塑料细杆，乙同学选择了一金属细杆，从提高实验精度的角度看，你认为                 （选填“甲”或“乙”）的选择较好；

金属细杆与塑料细杆相比重力较大，下落过程中空气阻力的影响较小，实验误差较小，应选择金属细杆做实验，故乙同学的选择较好。

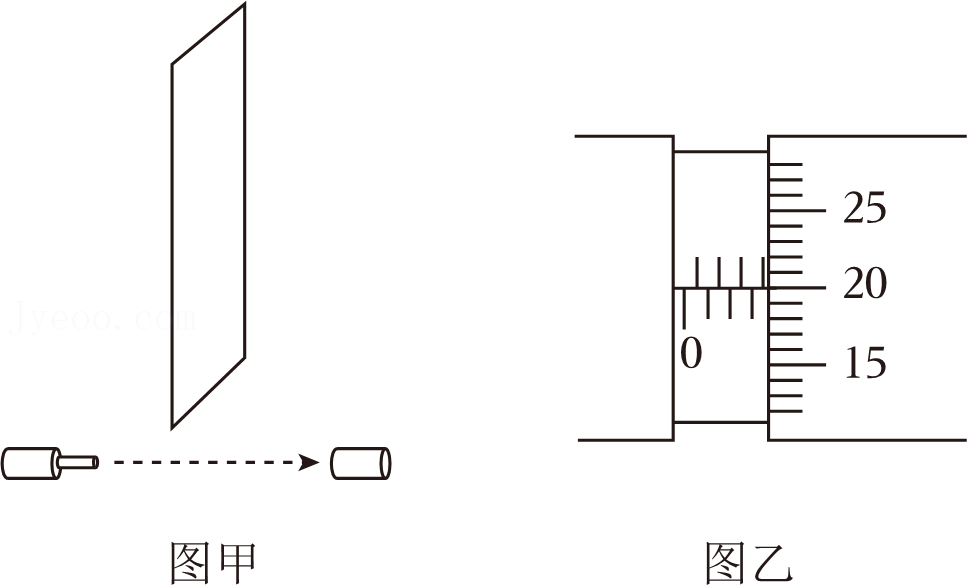
某同学测量金属杆的直径$d_{1}$，如图乙所示，其值为                 $\;\rm mm$；

螺旋测微器的精度值为$0.01\;\rm mm$，如图乙所示螺旋测微器的读数，即金属杆的直径$d_{1}$的值为：$d_{1}=3.5\;\rm mm+20.0\times 0.01\;\rm mm=3.700\;\rm mm$。

该同学利用$v_{1} = \dfrac{d_{1}}{t_{1}}$、$v_{2} = \dfrac{d_{1}}{t_{2}}$，分别求出下、上边框的经过光电门时的速度，测出上下边框两杆中心之间的距离$d_{2}$，在误差范围内，若$gd_{2}=$                 ，可判断机械能是否守恒。

下、上边框的经过光电门的过程，矩形框的重力势能减少量为：$\Delta E_{p}=mgd_{2}$

矩形框的动能增加量为：$\Delta E_{k} = \dfrac{1}{2}mv_{2}^{2} - \dfrac{1}{2}mv_{1}^{2} = \dfrac{1}{2}md_{1}^{2}(\dfrac{1}{t_{2}^{2}} - \dfrac{1}{t_{1}^{2}})$

若机械能守恒，则有：$\Delta E_{p}=\Delta E_{k}$

联立可得：$gd_{2}= \dfrac{d_{1}^{2}(t_{1}^{2} - t_{2}^{2})}{2t_{1}^{2}t_{2}^{2}}$，可判断机械能是守恒的。

本实验在下面的操作中，你认为正确的是 $(\quad\ \ \ \ )$

释放时框的下沿必须与光电门在同一高度

释放时框的下沿可以在光电门上方一定距离处

挡板下落时框如果没有保持竖直状态，对测量结果没有影响

$\rm AB$、根据以上分析，释放时框的下沿只要不在光电门下方即可。释放时框的下沿可以与光电门在同一高度，这样初动能为零。故$\rm A$错误，$\rm B$正确；

$\rm C$、下落时框没有保持竖直状态，那么框的下、上边经过光电门的过程，框下落的高度小于上下边框两杆中心之间的距离$d_{2}$，对测量结果有影响，故$\rm C$错误。

有同学提出细杆直径较大可能会对实验结果产生影响，若本实验忽略其他因素的影响，仅考虑直径较大对本实验的影响，本实验得出的重力势能的减小量和动能的增加量的关系为$\Delta E_{p}$                 $\Delta E_{k}$（选填“$\gt $”“$\lt $”或者“$=$”）。

利用光电门测量得到的速度是细杆通过光电门的平均速度，矩形框做匀变速直线运动，细杆通过光电门的平均速度等于该过程中间时刻的瞬时速度，而实验测出的上下边框两杆中心之间的距离$d_{2}$，此距离对应的初末速度应该是两杆中心通过光电门的瞬时速度，即细杆通过光电门的过程中的位移中点的瞬时速度。

根据匀变速直线运动推论可得：平均速度为：$\overline{v} = \dfrac{v_{0} + v_{t}}{2}$，位移中点的瞬时速度为：$v_{\dfrac{x}{2}} = \sqrt{\dfrac{v_{0}^{2} + v_{t}^{2}}{2}}$

设边框的下面的细杆通过光电门的初末速度分别为$v_{3}$、$v_{4}$，边框的上面的细杆通过光电门的初末速度分别为$v_{5}$、$v_{6}$。由运动学公式得：

$(\dfrac{v_{5} + v_{6}}{2})^{2} - (\dfrac{v_{3} + v_{4}}{2})^{2} =2ah$

$(\sqrt{\dfrac{v_{5}^{2} + v_{6}^{2}}{2}})^{2} - (\sqrt{\dfrac{v_{3}^{2} + v_{4}^{2}}{2}})^{2} =2ad_{2}$

整理可得：$\dfrac{v_{5}^{2} + v_{6}^{2}}{4} - \dfrac{v_{3}^{2} + v_{4}^{2}}{4} + \dfrac{v_{5}v_{6} - v_{3}v_{4}}{2} =2ah$……①

$\dfrac{v_{5}^{2} + v_{6}^{2}}{2} - \dfrac{v_{3}^{2} + v_{4}^{2}}{2} =2ad_{2}$……②

②式减去①式得：$\dfrac{v_{5}^{2} + v_{6}^{2}}{4} - \dfrac{v_{3}^{2} + v_{4}^{2}}{4} - \dfrac{v_{5}v_{6} - v_{3}v_{4}}{2} =2a(d_{2}﹣h)$

整理可得：$\dfrac{1}{4}[(v_{6}﹣v_{5})^{2}﹣(v_{4}﹣v_{3})^{2}]=2a(d_{2}﹣h)$

由：$v_{6}﹣v_{5}=at_{2}$，$v_{4}﹣v_{3}=at_{1}$，$t_{2}\lt t_{1}$，可得：$(v_{6}﹣v_{5})^{2}﹣(v_{4}﹣v_{3})^{2}\lt 0$，即$h\gt d_{2}$，

这说明光电门测出的两个瞬时速度对应的下落高度$h$大于实验测出的上下边框两杆中心之间的距离$d_{2}$，故本实验得出的重力势能的减小量和动能的增加量的关系为$\Delta E_{p}\lt \Delta E_{k}$。