如图甲所示，光滑水平面上有一质量$M=1\;\rm kg$的木板$A$，板左端有一质量$m=0.5\;\rm kg$的物块$B$（视为质点），$A$与$B$间的动摩擦因数为$0.2$，初始时均处于静止状态，仅给物块$B$施加水平向右的力$F$，$F$随时间$t$变化的图像如图乙所示，$1\;\rm s$末撤去$F$，物块$B$始终未从木板$A$上滑下。取$g=10\;\rm m/s^{2}$，最大静摩擦力与滑动摩擦力相等，则$(\qquad)$

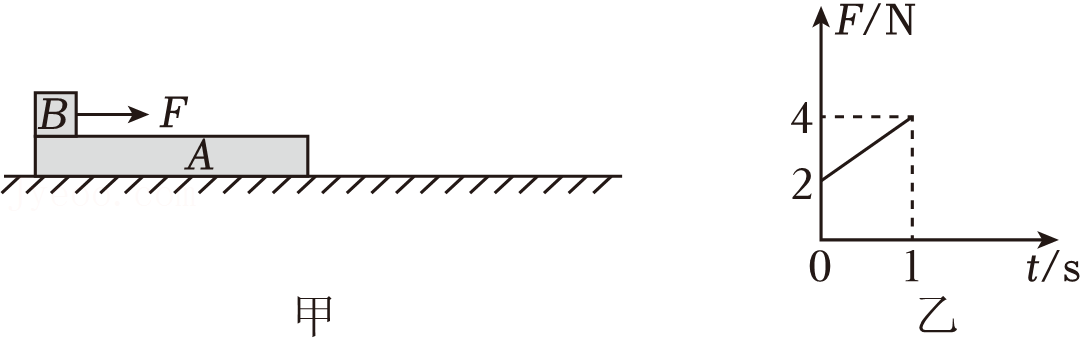
$1\\;\\rm s$时物块$B$的加速度大小为$4\\;\\rm m/s^{2}$

$1\\;\\rm s$时物块$B$的速度大小为$2\\;\\rm m/s$

$1\\;\\rm s$后木板$A$与物块$B$因摩擦产生的热量为$1.5\\;\\rm J$

木板$A$的长度可能为$1.5m$

$\rm A$、共速前对$A$分析，$\mu mg=Ma_{1}$，可得$A$木板最大加速度为$a_{1}=1\;\rm m/s$，假设开始运动时$A$、$B$同步加速运动，看作整体，$F=(M+m)a$，由题知$0﹣1\;\rm s$内，$F\gt 2\;\rm N$，故$a\gt \dfrac{4}{3}\;\rm m/s\gt a_{1}$，所以假设不成立，$A$、$B$在$0﹣1\;\rm s$内不同步加速，在$1\;\rm s$时$B$物块的运用牛顿第二定律，$F﹣\mu mg=ma_{2}$，解得$a_{2}=6\;\rm m/s$，故$\rm A$错误；

$\rm B$、根据$\rm A$选项分析，故$\rm B$错误；

$\rm C$、$A$在$0﹣1\;\rm s$内做匀加速直线运动，$v_{1}=a_{1}t$，解得$v_{1}=1\;\rm m/s$，$B$在$0﹣1\;\rm s$内做变加速直线运动，根据动量定理，$Ft﹣\mu mgt=mv_{2}$，$F﹣t$图的面积即为冲量，解得$v_{2}=4\;\rm m/s$，$A$、$B$最终共速，运用用动量守恒，$Mv_{1}+mv_{2}=(M+m)v_{共}$，再对$A$、$B$整体用能量守恒，$Q = \dfrac{1}{2}Mv_{1}^{2} + \dfrac{1}{2}mv_{2}^{2} - \dfrac{1}{2}(M + m)v_{共}^{2}$，解得$Q=1.5\;\rm J$，故$\rm C$正确；

$\rm D$、根据$\rm C$选项分析可知$1\;\rm s$后$A$、$B$因摩擦产生的热量$Q=1.5\;\rm J$，根据摩擦产生热量计算公式$Q=\mu mgx_{相对}$，可得$1\;\rm s$后$A$、$B$相对位移$x_{相对}=1.5\;\rm m$，根据$\rm A$选项分析可知在$0﹣1\;\rm s$内$A$、$B$也在相对运动，且相对运动方向与$1\;\rm s$后一致，所以木板的长度一定大于$1.5m$，故$\rm D$错误。

故选：$\rm C$。