| 动量守恒之木板滑块模型 题目答案及解析
稿件来源:高途
| 动量守恒之木板滑块模型题目答案及解析如下,仅供参考!
选修3-5
第十六章 动量守恒定律
16.3 动量守恒定律
动量守恒之木板滑块模型
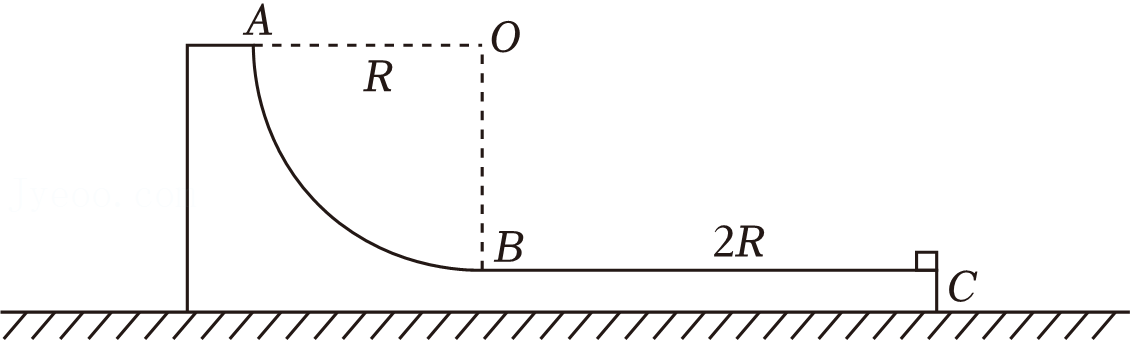
如图所示,轨道的上表面由长度为$2R$的水平部分$CB$和半径为$R$的四分之一光滑圆弧$AB$组成,轨道质量为$2m$,静止于光滑的水平地面上。一质量为$m$的小滑块(看作质点)从$C$点开始沿$CB$面水平向左运动,$CB$面与小滑块之间的动摩擦因数为$\mu $,重力加速度大小为$g$。要使滑块能越过$B$点滑上圆弧$AB$,求:
滑块运动到$B$点的过程中产生的热量;
滑块运动到$B$点的过程中产生的热量$2\\mu mgR$
"]]滑块运动到$B$点的过程中产生的热量为
$Q=\mu mg\cdot 2R=2\mu mgR$
滑块在$C$点的初速度$v_{0}$满足的条件。
滑块在$C$点的初速度满足$v_{0}\\gt \\sqrt{6\\mu gR}$
"]]滑块在水平轨道上向左做匀减速直线运动,滑块恰好到达$B$点时与轨道共速,取向左为正方向,由能量守恒定律和动量守恒定律得$\mu mg \cdot 2R = \dfrac{1}{2}mv_{0}^{2} - \dfrac{1}{2}(2m + m)v_{B}^{2}$
$mv_{0}=(2m+m)v_{B}$
联立解得$v_{0} = \sqrt{6\mu gR}$
要使滑块能越过$B$点滑上圆弧$AB$,滑块在$C$点的初速度应满足$v_{0}\gt \sqrt{6\mu gR}$
若滑块在$C$点的初速度$v_{0}$,求滑块滑上圆弧$AB$后能达到的最大高度。
滑块滑上圆弧$AB$后能达到的最大高度$\\dfrac{2}{3}\\mu R$
"]]滑块滑上圆弧$AB$后当滑块和轨道共速时,滑块达到最大高度$h$,取向左为正方向,由系统水平方向动量守恒和能量守恒可得
$mv_{0}=(m+2m)v_{共}mgh = \dfrac{1}{2}mv_{0}^{2} - \dfrac{1}{2}(m + 2m)v_{共}^{2} - \mu mg \cdot 2R$
解得滑块滑上圆弧$AB$后能达到的最大高度为$h = \dfrac{2}{3}\mu R$
| 动量守恒之木板滑块模型题目答案及解析(完整版)
