高中 | 闭合电路的欧姆定律基本问题 题目答案及解析
稿件来源:高途
高中 | 闭合电路的欧姆定律基本问题题目答案及解析如下,仅供参考!
选修3-1
第二章 恒定电流
2.7 闭合电路的欧姆定律
闭合电路的欧姆定律基本问题
如图所示,间距为$L$且足够长的光滑平行导轨上方连接阻值为$R$的电阻,导轨与水平面间的夹角为$\theta$,空间存在垂直于导轨平面向下、磁感应强度大小为$B$的匀强磁场。将质量为$m$、电阻为$r$、金属棒长度稍大于导轨间距,与导轨相交于$AA^\prime$的金属棒由静止释放,金属棒在运动过程中始终与导轨垂直且接触良好,导轨电阻不计,重力加速度大小为$g$,求:
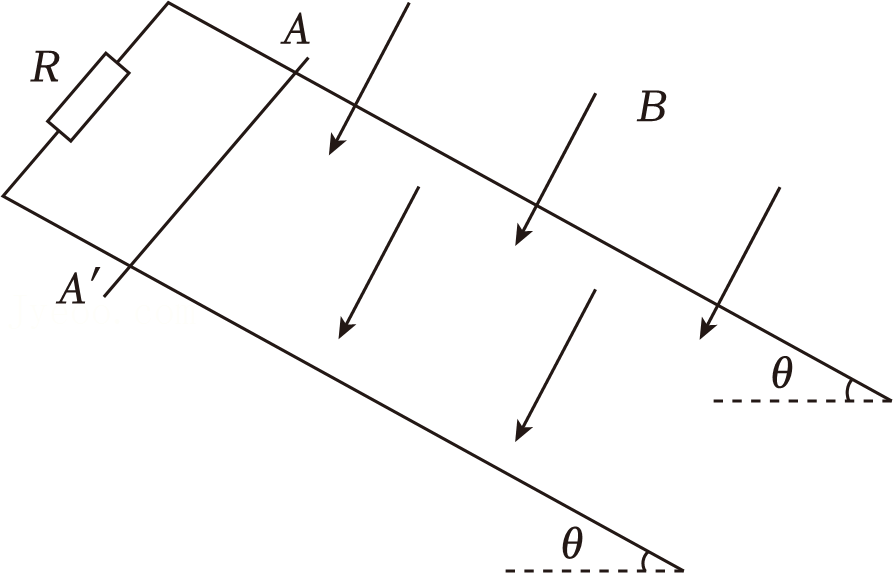
金属棒的最大速度$v_{m}$;
金属棒的最大速度为$\\dfrac{mg(R + r)\\sin\\theta}{B^{2}L^{2}}$
"]]当金属棒加速度为零时,速度最大,则
$mg\sin g\theta=BIL$
又金属棒产生的感应电动势为
$E=BLv_{m}$
电路中的电流$I = \dfrac{E}{R + r}$
联立可得$v_{m} = \dfrac{mg(R + r)\sin\theta}{B^{2}L^{2}}$
金属棒在斜面上稳定运动后,金属棒上$AA^\prime$两点间的电压$U_{AA^\prime}$。
金属棒在斜面上稳定运动后,金属棒上$AA^\\prime$两点间的电压为$\\dfrac{mgR\\sin\\theta}{BL}$
"]]金属棒在斜面上稳定运动后,金属棒两端的电压$U_{AA^\prime}$,为路端电压
$U_{AA^\prime}=IR$
可得$U_{AA'} = \dfrac{mgR\sin\theta}{BL}$
高中 | 闭合电路的欧姆定律基本问题题目答案及解析(完整版)
