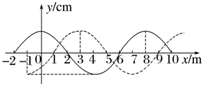
该波波长；

该波波长为$8\\;\\rm m$

由图可知，该波的波长$\lambda=8\;\rm m$

若已知波向$x$轴正方向传播，求波的最大周期；

若已知波向$x$轴正方向传播，波的最大周期为$\\dfrac{4}{3}\\;\\rm s$

若已知波向$x$轴正方向传播，结合波的周期性可得

$t=nT+ \dfrac{3}{8}T$，（$n=0$，$1$，$2$，$3$…）

得

$T= \dfrac{4}{8n + 3}\;\rm s$，（$n=0$，$1$，$2$，$3$…）

当$n=0$时，$T$最大，且$T_{\max}= \dfrac{4}{3}\;\rm s$

若波的传播方向未知，求波速的表达式。

若波向$x$轴正方向传播，波速为（$16n+6)\\;\\rm m/s$，（$n=0$，$1$，$2$，$3$…）；若波向$x$轴负方向传播，波速为$(16n+10)\\;\\rm m/s$，（$n=0$，$1$，$2$，$3$…）

若波向$x$轴正方向传播，波传播的距离为

$\Delta x=(n\lambda+3)m=(8n+3)\;\rm m$，（$n=0$，$1$，$2$，$3$…）

故波速为

$v= \dfrac{\Delta x}{t} = \dfrac{8n + 3}{0.5}\;\rm m/s=(16n+6)\;\rm m/s$，（$n=0$，$1$，$2$，$3$…）。

若波向$x$轴负方向传播，波传播的距离为

$\Delta x=(n\lambda+5)\;\rm m=(8n+5)\;\rm m$，（$n=0$，$1$，$2$，$3$…）

故波速为

$v= \dfrac{\Delta x}{t} = \dfrac{8n + 5}{0.5}\;\rm m/s=(16n+10)\;\rm m/s$，（$n=0$，$1$，$2$，$3$…）