| 斜面问题 题目答案及解析
稿件来源:高途
| 斜面问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
斜面问题
如图所示,倾角$\theta=37^\circ$的斜面固定在水平面上。质量$m=1.0\;\rm kg$的小物块受到沿斜面向上的$F=9.0\;\rm N$的拉力作用,小物块由静止沿斜面向上运动。小物块与斜面间的动摩擦因数$\mu=0.25$。(斜面足够长,取$g=10\;\rm m/s^{2}$,$\sin37^\circ=0.6$,$\cos37^\circ=0.8$)
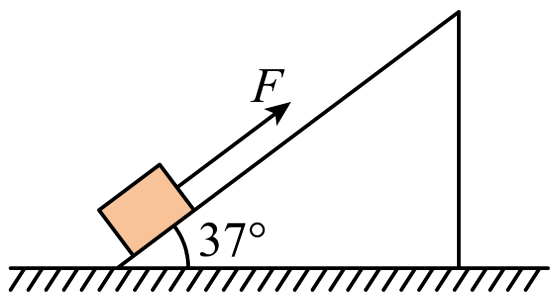
求在拉力的作用过程中,小物块加速度的大小;
[["
$1\\;\\rm m/s^{2}$
"]]对小物块进行受力分析,根据牛顿第二定律有
$F-f-mg\sin\theta=ma_{1}$
$f=\mu mg\cos\theta$
代入数据有$a_{1}=1\;\rm m/s^{2}$
若在小物块沿斜面向上运动$0.80\;\rm m$时,将拉力$F$撤去,求此后小物块沿斜面向上运动的距离。
[["
$0.1\\;\\rm m$
"]]设撤去拉力前小物块运动的距离为$x_{1}$,撤去拉力时小物块的速度为$v$,根据匀变速直线运动速度与位移的关系有$v^{2}=2a_{1}x_{1}$
撤去拉力后小物块加速度和向上运动的距离大小分别为$a_{2}$、$x_{2}$,有$f+mg\sin\theta=ma_{2}$
再根据匀变速直线运动速度与位移的关系有$0-v^{2}=-2a_{2}x_{2}$
代入数据有$x_{2}=0.1\;\rm m$
| 斜面问题题目答案及解析(完整版)
去刷题
相关题库:
某同学为了测定木块与斜面间的动摩擦因数,他用测速仪研究木块在斜面上的运动情况,装置如图甲所示,他使木块以初速度的速度沿倾角的斜面上滑紧接着下滑至出发点,并同时开始记录数据,结果电脑只绘出了木块从开始上滑至最高点的图线如图乙所示,取,则根据题意计算出的下列物理量正确的是
如图所示,固定光滑斜面长为,为斜面中点。一物块在恒定拉力作用下,从最低点由静止开始沿斜面向上拉到点撤去拉力,物块继续上滑经过最高点,设物块由运动到的时间为,下列描述该过程中物块的速度随时间、物块的动能随位移、机械能随位移、加速度随位移变化规律的图像中,可能正确的是
可爱的企鹅喜欢在冰面上玩游戏。如图所示,有一企鹅在倾斜冰面上,先以加速度从冰面底部由静止开始沿直线向上“奔跑”,时,突然卧倒以加速度大小为肚皮贴着冰面匀减速向前滑行,直到最高点。求:
为了研究滑板运动中的滑道设计,如图所示,将滑道的竖直截面简化为直轨道与圆弧轨道,半径与垂直,两点的高度差,两点的高度差,段动摩擦因数,段摩擦不计,圆弧半径,运动过程空气阻力不计,与水平方向的夹角。将运动员及滑板简化为一质量的质点,经过前一滑道的滑行,到达图示的点时速度恰好水平向右,到达点时速度恰好与斜面平行进入斜面,经过后竖直上抛再从点落回滑道,取。求:
用长度为的铁丝绕成一个高度为的等螺距螺旋线圈,将它竖直地固定于水平桌面。穿在铁丝上的一小珠子可沿此螺旋线圈无摩擦地下滑(下滑过程线圈形状保持不变),已知重力加速度为。这个小珠子从螺旋线圈最高点无初速滑到桌面经历的时间和速度分别为
今日推荐 ![]()
![]()
![]()
