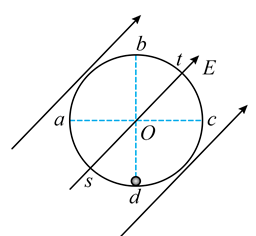
如图所示，半径为$r$的内壁光滑的绝缘轨道沿竖直方向固定，整个空间存在与水平方向成$45^{\circ}$的匀强电场，其电场强度大小为$E=\dfrac{\sqrt{2}mg}{q}$，图中$a$、$c$两点与圆心等高，$b$、$d$分别为圆轨道的最高点和最低点，$s$、$t$两点分别为弧$ad$和弧$bc$的中点。一质量$m$、电荷量为$+q$的小球在圆轨道内侧的$d$点获得一初速度，结果小球刚好能在圆轨道内做完整的圆周运动，规定$d$点的电势为$0$，重力加速度为$g$。下列说法正确的是$(\quad\ \ \ \ )$

小球在$t$点时小球动能最小

小球在$d$点获得的速度大小为$\\sqrt{3gr}$

小球电势能的最大值为$\\left( \\sqrt{2}-1\\right)mgr$

小球在$a$、$c$两点对轨道的压力差大小为$6mg$

$\rm A$．小球在电场中受到的电场力为$F=qE=\sqrt{2}mg$，则在竖直方向上${{F}_{y}}=F\sin 45{}^\circ =mg$，即电场力在竖直方向的分力与重力平衡，在水平方向的分力为小球所受到的合力${{F}_{合}}={{F}_{x}}=F\cos 45{}^\circ =mg$，所以，小球等效受到水平向右的等效重力，等效重力大小为${G}'={{F}_{合}}=mg$，所以，$a$点为等效最高点，动能最小，故$\rm A$错误；

$\rm B$．小球在等效最高点等效重力恰好提供向心力时，小球刚好能在圆轨道内做完整的圆周运动，此时根据牛顿第二定律${G}'=m\dfrac{v_{a}^{2}}{r}$，解得${{v}_{a}}=\sqrt{gr}$，则小球由$d$到$a$的过程，根据动能定理$-{G}'r=\dfrac{1}{2}mv_{a}^{2}-\dfrac{1}{2}mv_{d}^{2}$，解得$v=\sqrt{3gr}$，故$\rm B$正确；

$\rm C$．根据${{E}_{\text{p}}}=q\varphi $可知，带正电的小球所在位置的电势越高，电势能越大，由题意可知，小球在$s$点时电势最高，电势能最大。又因为$d$点电势为$0$。则${{U}_{sd}}=E{{d}_{sd}}=Er\left( 1-\sin 45{}^\circ \right)=\dfrac{\left( \sqrt{2}-1 \right)mgr}{q}={{\varphi }_{s}}-{{\varphi }_{d}}$，则$s$点的电势为$\varphi_{s}=\dfrac{\left( \sqrt{2}-1\right)mgr}{q}$，小球的电势能为$E_{\text{p}}=q\varphi_{s}=\left( \sqrt{2}-1\right)mgr$，故$\rm C$正确；

$\rm D$．由以上分析可知，$a$点为等效最高点，小球在等效最高点等效重力恰好提供向心力，此时轨道对小球的支持力为零，即${{N}_{a}}=0$，根据牛顿第三定律可知，小球对轨道的压力大小等于轨道对小球的支持力大小，即${{F}_{a}}={{N}_{a}}=0$，小球运动到$c$点，根据动能定理${G}'\times 2r=\dfrac{1}{2}mv_{c}^{2}-\dfrac{1}{2}mv_{a}^{2}$，小球在$c$点时，轨道对小球的支持力和小球等效重力的合力提供向心力${{N}_{c}}-{G}'=m\dfrac{v_{c}^{2}}{r}$，联立解得${{N}_{c}}=6mg$，根据牛顿第三定律可知，小球对轨道的压力大小等于轨道对小球的支持力大小，即${{F}_{c}}={{N}_{c}}=6mg$，则小球在$a$、$c$两点对轨道的压力差大小为$\text{ }\!\!\Delta\!\!\text{ }F={{F}_{c}}-{{F}_{a}}=6mg$，故$\rm D$正确。

故选$\rm BCD$。