高中 | 带电粒子在等效重力场中的运动 题目答案及解析
稿件来源:高途
高中 | 带电粒子在等效重力场中的运动题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
带电粒子在等效重力场中的运动
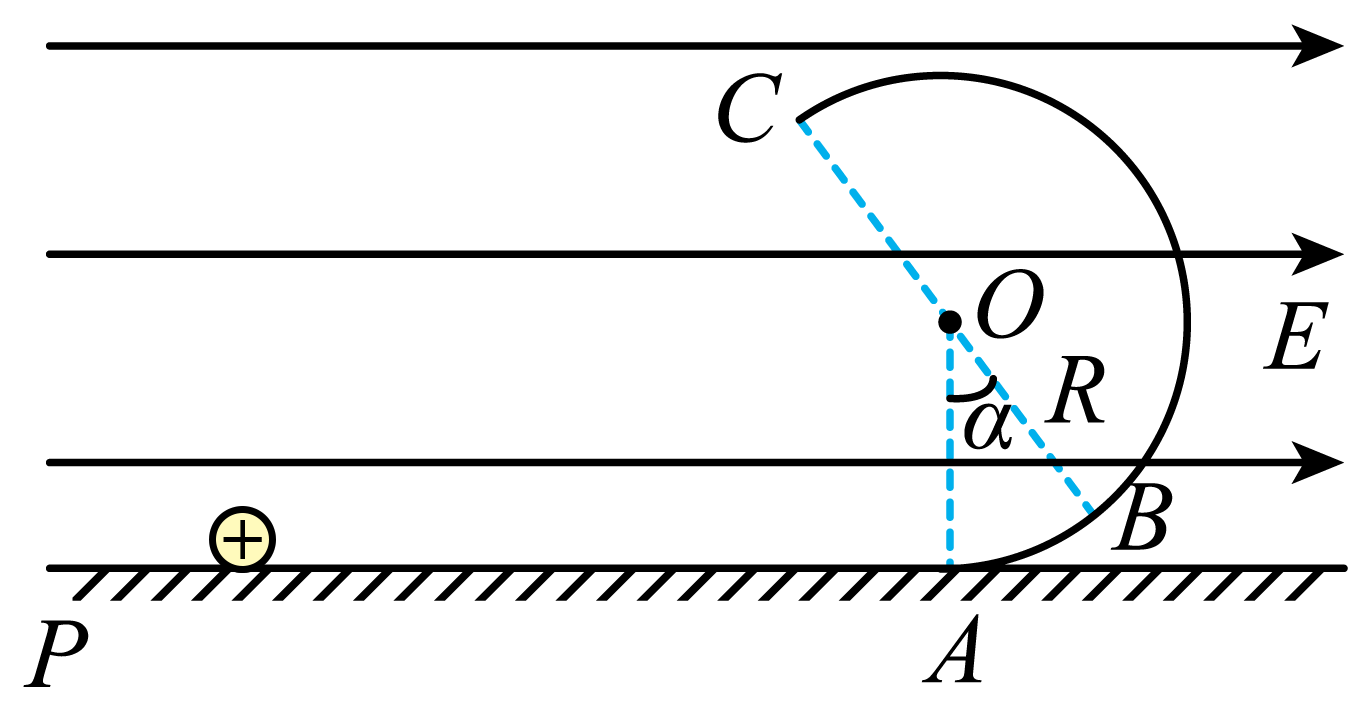
如图,在竖直平面内,一半径为$R$的光滑圆弧轨道$ABC$与光滑水平轨道$PA$相切于$A$点,$BC$为圆弧轨道$ABC$的直径,$O$为圆心,$OA$和$OB$之间的夹角$\alpha = 37^\circ $。整个装置处于水平向右的匀强电场中。一质量为$m$、电荷量为$q(q \gt 0)$的带电小球(可视为质点)可以在圆弧轨道上的$B$点保持静止。现将该带电小球从水平轨道某点静止释放,小球经$A$点沿圆弧轨道$ABC$恰好能通过$C$点。已知重力加速度大小为$g$,$\sin 37^\circ = 0.6, \cos 37^\circ = 0.8$。求:
匀强电场的电场强度$E$的大小;
$E = \\dfrac{3mg}{4q}$;
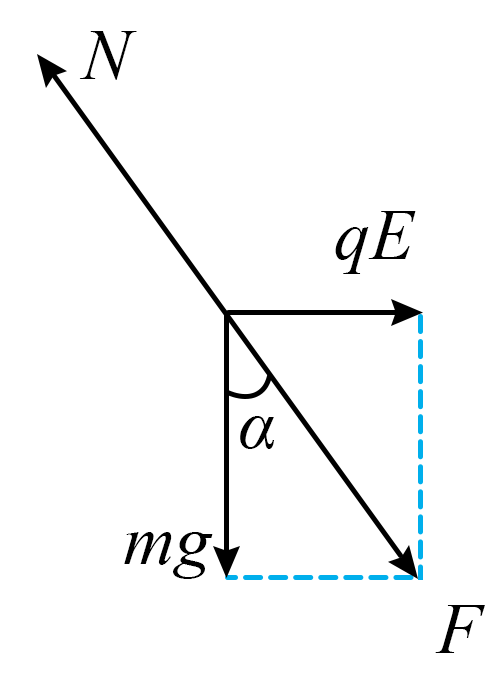
"]]小球可以在圆弧轨道上的$B$点保持静止,小球受合力为$0$
$\tan\alpha = \dfrac{qE}{mg}$
解得$E = \dfrac{3mg}{4q}$
小球经过$C$点时,电场力对小球做功的功率$P$;(结果保留根号)
$P = - \\dfrac{3mg}{10}\\sqrt{5gR}$;
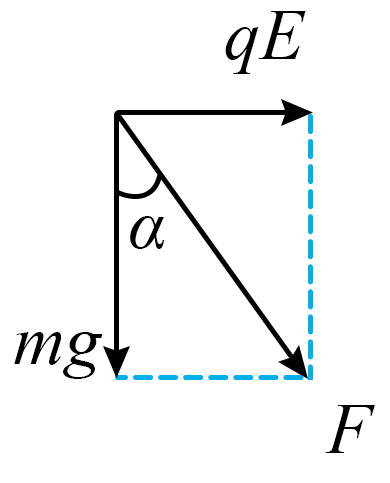
"]]小球到达$C$点时受重力和电场力作用,合力的大小为$F$$\cos\alpha = \dfrac{mg}{F}$
设小球到达$C$点时的速度大小为$v_{C}$,由牛顿第二定律得$F = m\dfrac{{v_{C}}^{2}}{R}$
小球在$C$点电场力与速度夹角为$143^\circ $,故小球在$C$点所受电场力做功的功率$P = qE ⋅ v_{C}\cos 143^\circ $
解得$P = - \dfrac{3mg}{10}\sqrt{5gR}$
小球在圆弧轨道上运动时对轨道的最大压力的大小。
$F_{压} = \\dfrac{15}{2}mg$
"]]在$B$点,重力和电场力的合力$F$沿$OB$方向背离圆心,小球对圆弧轨道的压力最大。
$B$到$C$过程,由动能定理得$- F \cdot 2R = \dfrac{1}{2}m{v_{C}}^{2} - \dfrac{1}{2}m{v_{B}}^{2}$
在$B$点,由牛顿第二定律得$N_{B} - F = m\dfrac{{v_{B}}^{2}}{R}$
解得$N_{B} = \dfrac{15}{2}mg$
由牛顿第三定律得:小球在圆弧轨道上运动时对轨道的最大压力为$F_{压} = N_{B} = \dfrac{15}{2}mg$
高中 | 带电粒子在等效重力场中的运动题目答案及解析(完整版)
