回旋加速器的主要结构如图所示，两个$D$形金属盒间接高频交流电源，且两金属盒置于与盒面垂直的匀强磁场中，两金属盒间的狭缝宽度很小。粒子源$S$位于金属盒的圆心处，粒子源射出的粒子的初速度可以忽略。现用回旋加速器分别加速两种不同的粒子$a$、$b$，$a$、$b$的质量之比为$1:4$，电荷量之比为$1:2$，已知狭缝间的加速电压大小恒为$U$，磁场的磁感应强度大小为$B$，$D$形金属盒的半径为$R$，狭缝之间的加速距离为$d$。不计粒子受到的重力，则$(\qquad)$

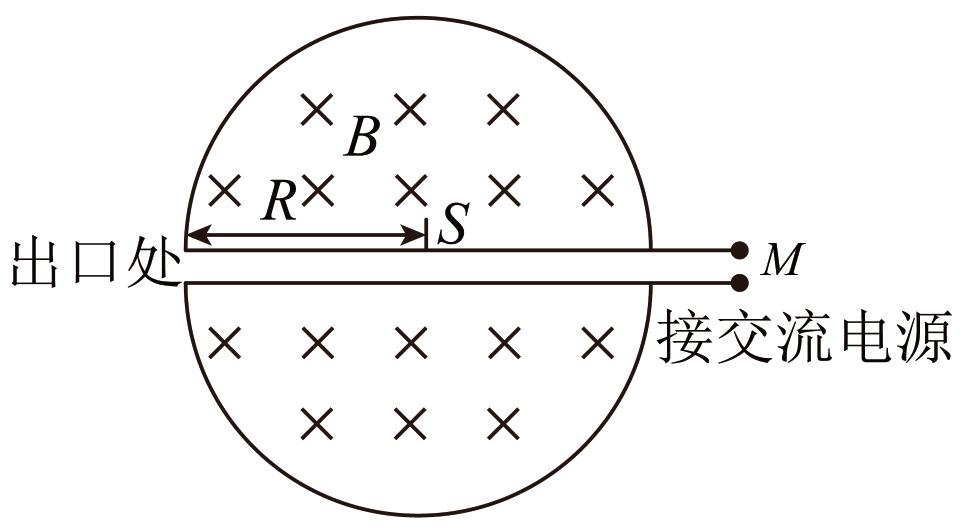
要使粒子$a$、$b$每经过狭缝都被加速，交变电压的频率不相同

粒子$a$、$b$所能达到的最大动能相等

粒子$a$、$b$在$D$形金属盒中运动第$n$个半圆的半径之比为$\\sqrt{2}:2$

粒子$a$、$b$在达到最大动能的过程中，通过狭缝的次数之比为$1:2$

$\rm A$．带电粒子在磁场中运动的周期与电场变化的周期相等，周期$T=\dfrac{2\pi m}{qB}$，与粒子的速度无关，交变电场的周期也为$T=\dfrac{2\pi m}{qB}$，频率为$f=\dfrac{1}{T}=\dfrac{qB}{2\pi m}$，因两粒子$a$、$b$比荷不相同，则交变电压的频率不相同，故$\rm A$正确；

$\rm B$．当粒子的半径到达$D$型盒的半径$R$时，速度最大，由公式$E_{\rm k}=\dfrac{1}{2}m{{v}^{2}}=\dfrac{{{B}^{2}}{{q}^{2}}{{R}^{2}}}{2m}$

可得，动能之比等于电荷量的平方之比与质量反比的积，所以所能达到的最大动能相等，故$\rm B$正确；

$\rm C$．带电粒子在$D$盒中第$n$个半圆，由动能定理和牛顿第二定律有

$nqU=\dfrac{1}{2}mv_{n}^{2}$，$q{{v}_{n}}B=\dfrac{mv_{n}^{2}}{{{r}_{n}}}$

得${{r}_{n}}=\dfrac{1}{B}\sqrt{\dfrac{2nmU}{q}}$

因两粒子$a$、$b$的质量之比为$1:4$，电荷量之比为$1:2$，所以第$n$个半圆的半径之比为$\sqrt{2}:2$，故$\rm C$正确；

$\rm D$．粒子每加速一次增加的动能为$qU$，粒子能达到的最大动能为

$nqU=E_{\rm k}=\dfrac{{{B}^{2}}{{q}^{2}}{{R}^{2}}}{2m}$

所以要加速的次速为$n=\dfrac{{{B}^{2}}q{{R}^{2}}}{2mU}$

所以在达到最大动能的过程中通过狭缝的次数之比为$2$：$1$，故$\rm D$错误。

故选：$\rm ABC$。