如图所示，三个完全相同的半圆形光滑绝缘轨道竖直放置，图乙、图丙分别置于匀强磁场$B$和匀强电场$E$中，轨道两端点在同一高度上。现将$a$、$b$、$c$三个相同的带正电小球同时从轨道左端的最高点由静止释放，小球均能经过轨道最低点。已知小球的带电荷量不会发生变化，则$a$、$b$、$c$三个小球$(\qquad)$

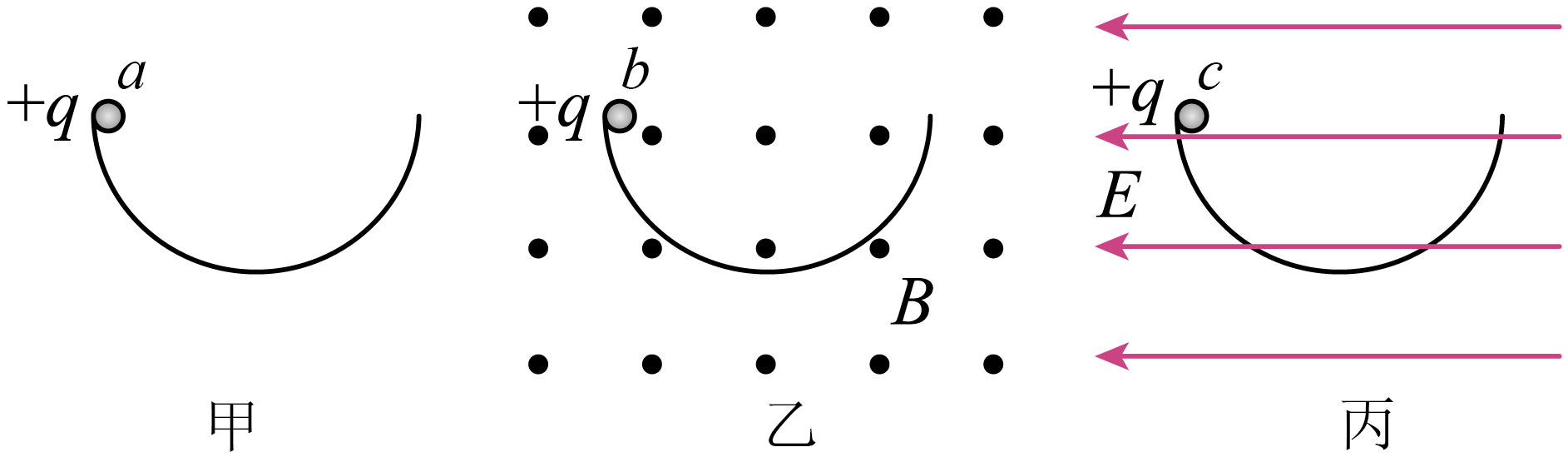
在向右运动过程中始终不会脱离轨道

到达轨道最低点时的速率均相同

向右经过轨道最低点时，$b$球对轨道的压力最大

向左经过轨道最低点时，$a$球对轨道的压力最小

$\rm A$．当小球从不高于圆心的位置由静止释放，其不会脱离轨道，所以在小球向右运动过程中始终不会脱离轨道，故$\rm A$项正确；

$\rm B$．对于$a$球，到达最低点有$mgR=\dfrac{1}{2}mv_{a}^{2}$

对于$b$球，由于洛伦兹力不做功，所以到达最低点有$mgR=\dfrac{1}{2}mv_{b}^{2}$

对于$c$球，由于电场力做功，所以到达最低点有$mgR-qER= \dfrac{1}{2}mv_{c}^{2}$

有上述式子分析可知，到达最低点时，$a$球和$b$球的速度大小相同，$c$球的速度大小小于$a$球和$b$球的速度大小，故$\rm B$项错误；

$\rm C$．向右经过最低点时，由牛顿第二定律，对$a$球有${{F}_{{N}a}}-mg=m\dfrac{v_{a}^{2}}{R}$

对于$b$球有${{F}_{{N}b}}-mg-q{{v}_{b}}B=m\dfrac{v_{b}^{2}}{R}$

对于$c$球有${{F}_{{N}c}}-mg=m\dfrac{v_{c}^{2}}{R}$

结合之前的分析有$v_{a}=v_{b}\gt v_{c}$，所以其$b$球对于轨道的压力最大，故$\rm C$项正确；

$\rm D$．向左经过最低点时，对$a$球有${{F}_{{N}a1}}-mg=m\dfrac{v_{a1}^{2}}{R}$

由于整个运动过程中，只有重力做功，重力做功只与始末位置高度差有关，所以${{v}_{a}}={{v}_{a1}}$

对于$b$球有${{F}_{{N}b1}}-mg+q{{v}_{b1}}B=m\dfrac{v_{b1}^{2}}{R}$

由于整个运动过程中，只有重力做功，重力做功只与始末位置高度差有关，所以${{v}_{b}}={{v}_{b1}}$

对于$c$球有${{F}_{{N}c1}}-mg=m\dfrac{v_{c1}^{2}}{R}$

由于整个运动过程只有重力和电场力做功，而电场力做功只与始末位置有关，重力做功只与始末位置高度差有关，所以有${{v}_{c}}={{v}_{c1}}$

结合上述分析可知，$b$球对轨道的压力小于$a$球对轨道的压力，所以$a$球不是对轨道的压力最小的，故$\rm D$项错误。

故选：$\rm AC$。