如图，质量为$m$、带电荷量为$+q$的小金属块$A$以初速度${{v}_{0}}$从光滑绝缘水平高台上飞出。已知在足够高的高台边缘右面空间中存在水平向左的匀强电场，场强大小$E=\dfrac{3mg}{q}$。则$(\qquad)$

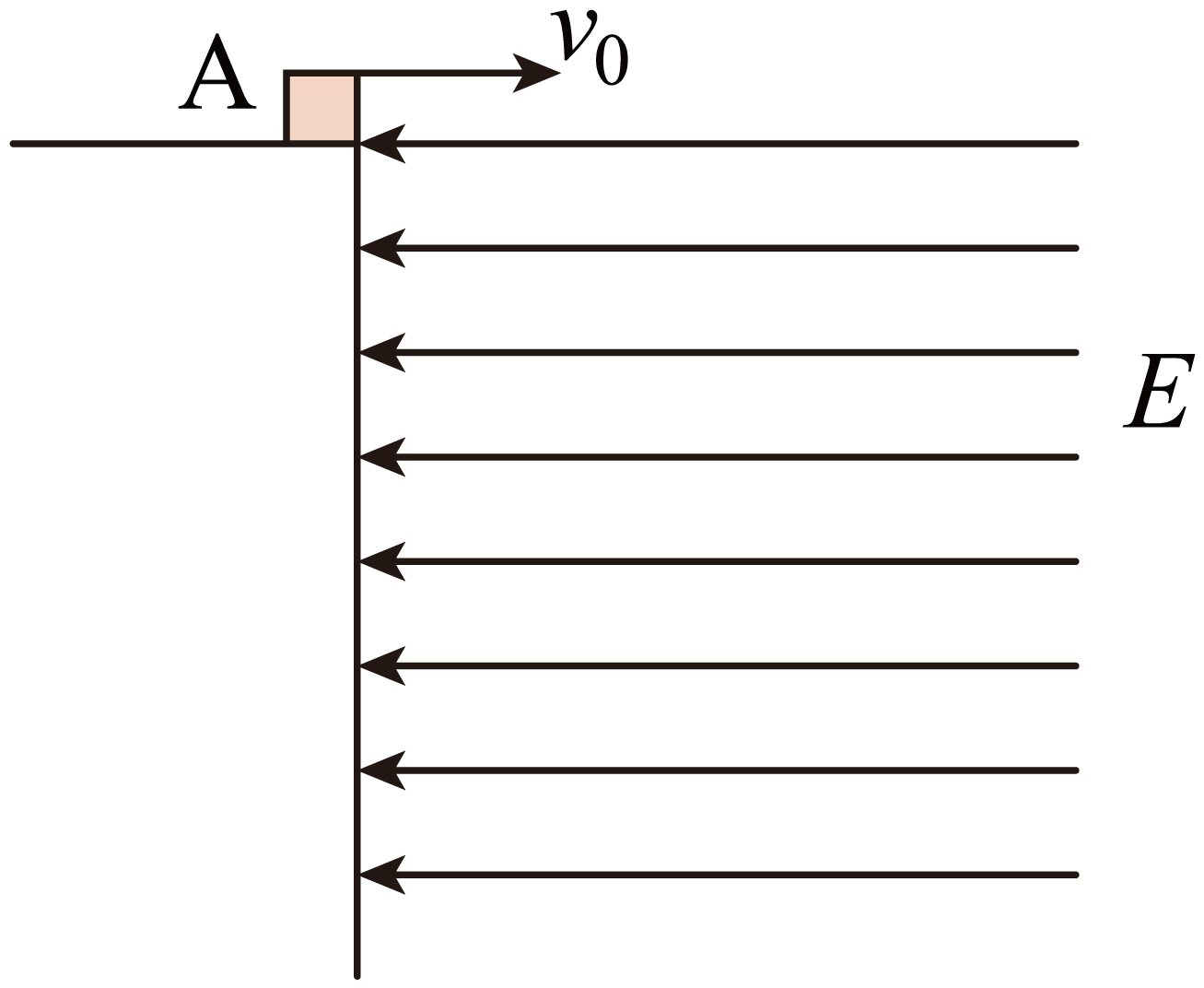
金属块不一定会与高台边缘相碰

金属块一定会与高台边缘相碰，相碰前金属块在做匀变速运动

金属块运动过程中距高台边缘的最大水平距离为$\\dfrac{v_{0}^{2}}{6g}$

金属块运动过程的最小速度为$\\dfrac{\\sqrt{10}{{v}_{0}}}{10}$

$\rm AB$．金属块在竖直方向上做自由落体运动，在水平方向先向右做匀减速运动，当速度减小到零后再向左做匀加速运动，一定能回到高台的边缘；在运动过程中，所受的电场力和重力的合力保持不变，因此做匀变速运动，$\rm A$错误，$\rm B$正确；

$\rm C$．在水平方向上，当向右运动的速度减小到零时，距离高台边缘最远，根据$v_{0}^{2}=2ax$

而$Eq=ma$

可得最大距离$x=\dfrac{v_{0}^{2}}{6g}$

$\rm C$正确；

$\rm D$．重力与电场力的合成为$F$，设合力与电场力方向的夹角为$\theta$，如图所示

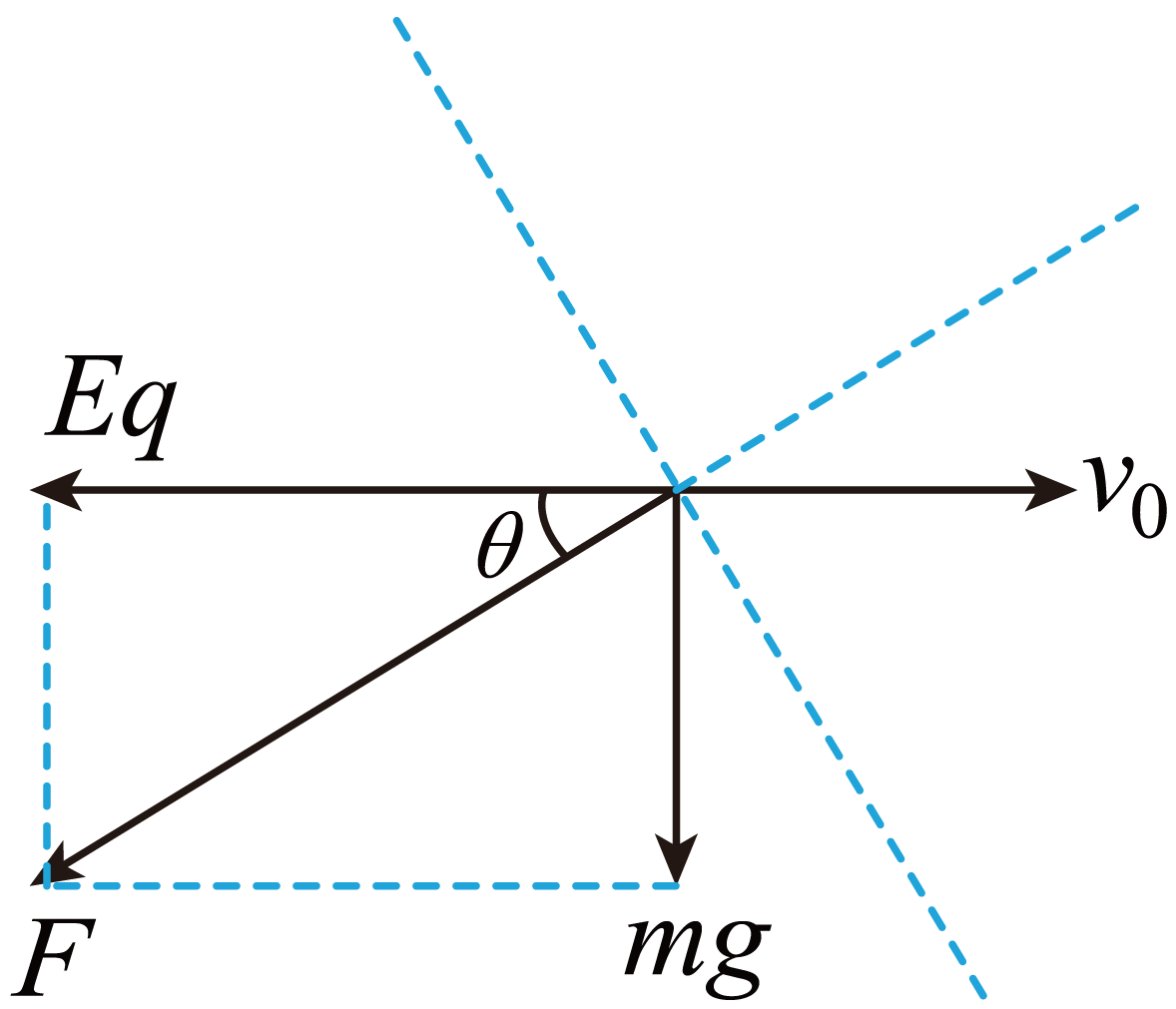
可知$\sin \theta =\dfrac{mg}{\sqrt{{{(Eq)}^{2}}+{{(mg)}^{2}}}}=\dfrac{\sqrt{10}}{10}$

将速度方向沿$F$的方向和垂直于$F$的方向正交分解，当沿$F$的方向速度减小到零时，速度达到最小值，最小值为$v={{v}_{0}}\sin \theta =\dfrac{\sqrt{10}{{v}_{0}}}{10}$

$\rm D$正确。

故选：$\rm BCD$。