高中 | 库仑定律的计算与应用 题目答案及解析
稿件来源:高途
高中 | 库仑定律的计算与应用题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.2 库仑定律
库仑定律的计算与应用
如图所示,电荷量均为$Q$的正点电荷$A$、$B$在同一水平线上;$GH$为与$A$、$B$连线在同一水平面的垂直平分线,悬点$O$位于$A$、$B$连线中点正上方。另有一个质量为$m$、电荷量为$+q$的带电小球$C$(可视为质点),用长为$L$的绝缘轻细线悬挂于$O$点。现在把小球$C$拉起到$M$点,使细线水平且与$G$、$H$处于同一竖直面内,由静止释放后,小球$C$运动到$GH$线上的$N$点时刚好速度为零,此时细线与竖直方向的夹角$\theta =30{}^\circ $。已知重力加速度为$g$,静电力常量为$k$,不计空气阻力,试求:
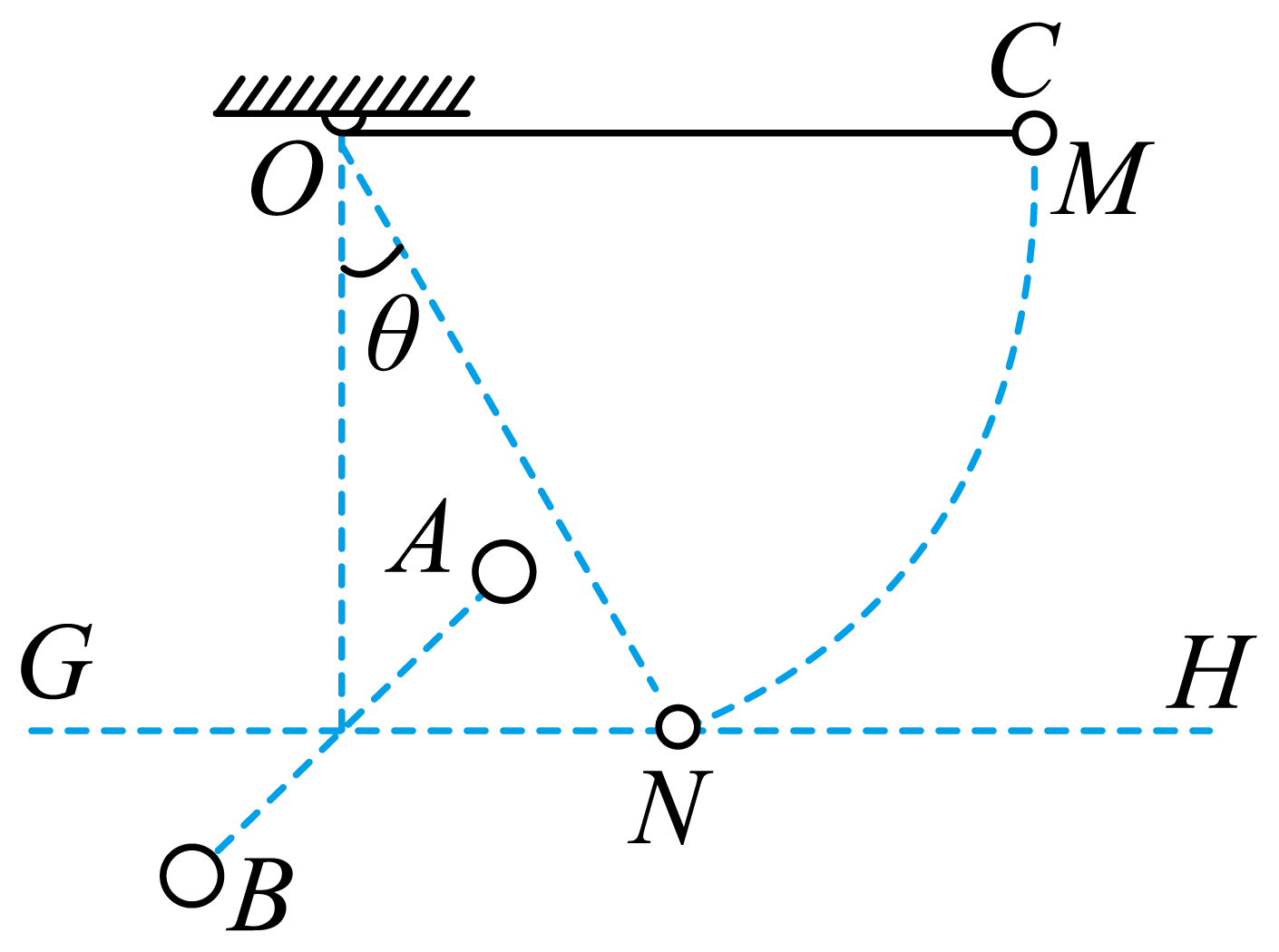
在$A$、$B$所形成的电场中,$M$、$N$两点间的电势差;
${{U}_{MN}}=-\\dfrac{\\sqrt{3}mgL}{2q}$;
"]]带电小球$C$在从$M$点运动到$N$点的过程中,由动能定理$mgL\cos 30{}^\circ +q{{U}_{MN}}=0$
解得${{U}_{MN}}=-\dfrac{mgL\cos 30{}^\circ }{q}=-\dfrac{\sqrt{3}mgL}{2q}$;
若$NA$、$NB$与$AB$连线的长度相等,则小球运动到$N$点瞬间,细线对小球的拉力${{F}_{{T}}}$的大小。
${{F}_{{T}}}=\\dfrac{\\sqrt{3}}{2}mg+\\dfrac{3\\sqrt{3}kQq}{2{{L}^{2}}}$
"]]在$N$点,小球$C$受力如图所示,
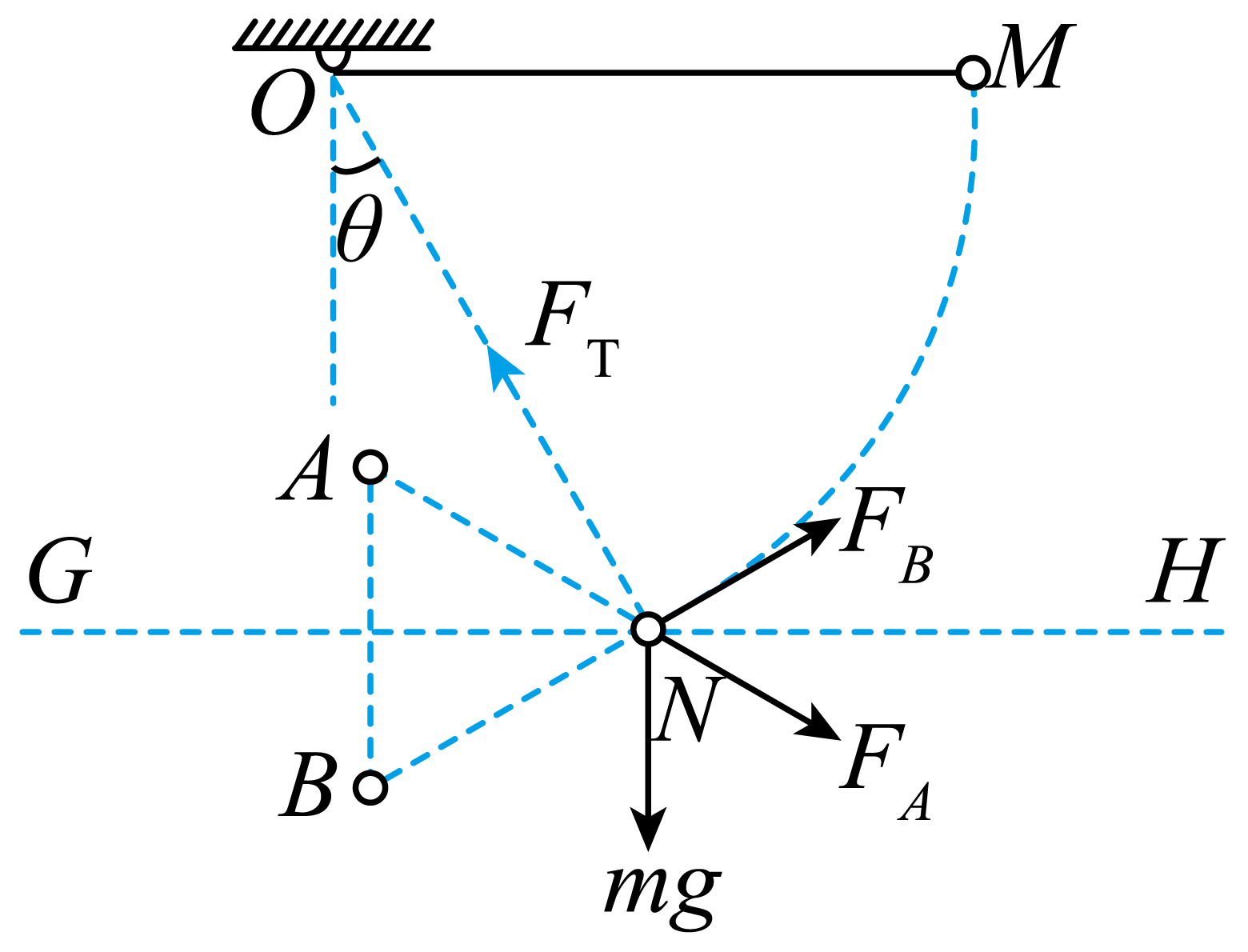
沿细线方向的合力为零,则${{F}_{{T}}}-mg\cos 30{}^\circ -2{{F}_{{A}}}\cos 30{}^\circ \cdot \cos 60{}^\circ =0$
又${{F}_{{A}}}={{F}_{{B}}}=k\dfrac{Qq}{{{\left( \dfrac{\sqrt{3}L}{3} \right)}^{2}}}$
解得${{F}_{{T}}}=mg\cos 30{}^\circ +k\dfrac{Qq}{{{R}^{2}}}\cos 30{}^\circ =\dfrac{\sqrt{3}}{2}mg+\dfrac{3\sqrt{3}kQq}{2{{L}^{2}}}$。
高中 | 库仑定律的计算与应用题目答案及解析(完整版)
