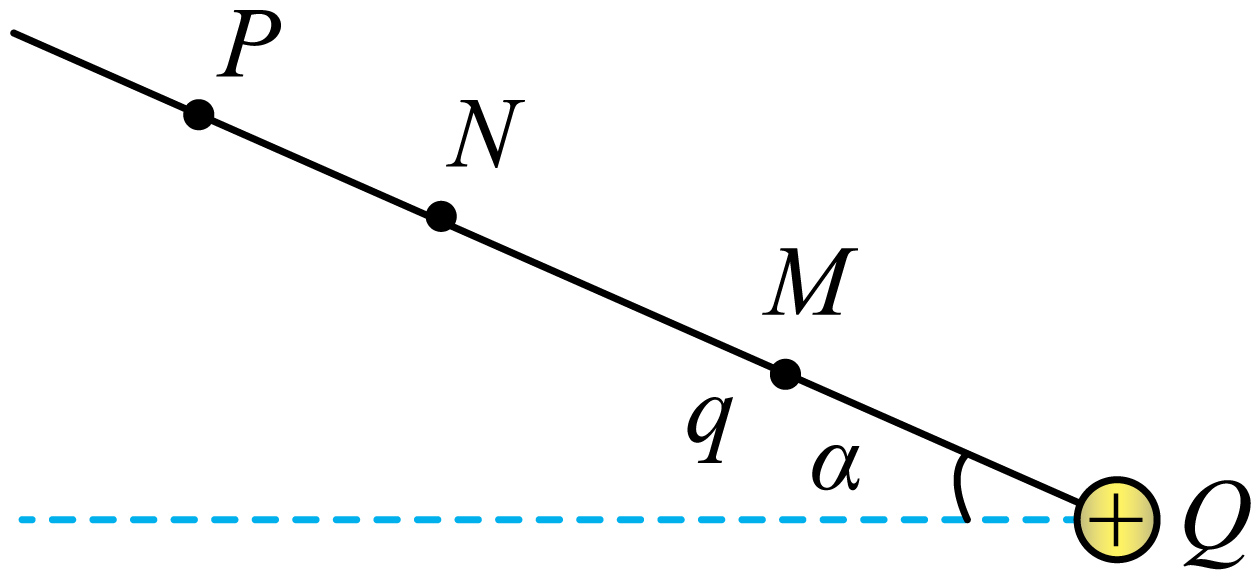
如图所示，竖直平面内足够长的光滑绝缘直杆与水平面的夹角$\alpha=30^\circ $，直杆的底端固定一电荷量为$Q$的带正电小球，$M$、$N$、$P$为杆上的三点。现将套在绝缘杆上有孔的带正电物块从直杆上的$M$点由静止释放。物块上滑到$N$点时速度达到最大，上滑到$P$点时速度恰好变为零。已知带电物块的质量为$m$、电荷量为$q$，$M$、$P$两点间的距离为$x$，静电力常量为$k$，不计空气阻力，重力加速度大小为$g$，带电体均可视为点电荷。则$N$点到直杆底端的距离$r$和$M$、$P$两点间的电势差$U_{MP}$分别为$(\qquad)$

$r=\\sqrt{\\dfrac{kQq}{mg}}$，$U_{MP}=\\dfrac{mgx}{2q}$

$r=\\sqrt{\\dfrac{kQq}{mg}}$，$U_{MP}=\\dfrac{mgx}{q}$

$r=\\sqrt{\\dfrac{2kQq}{mg}}$，$U_{MP}=\\dfrac{mgx}{2q}$

$r=\\sqrt{\\dfrac{2kQq}{mg}}$，$U_{MP}=\\dfrac{mgx}{q}$

带电物块上滑到$N$点时，受到的库仑力大小$F_{库}=k\dfrac{Qq}{r^{2}}$

带电物块上滑到$N$点时速度最大，此时带电物块所受的合外力等于零，根据受力平衡有$F_{库}=mg\sin\alpha$

解得$N$点到直杆底端的距离$r$，$r=\sqrt{\dfrac{2kQq}{mg}}$

带电物块从$M$点到$P$点，根据动能定理有

$−mgx\sin\alpha+W_{MP}=0$

$M$、$P$两点间的电势差$U_{MP}=\dfrac{W_{MP}}{q}$

解得$M$、$P$两点间的电势差为$U_{MP}=\dfrac{mgx}{2q}$

故选：$\rm C$。