高中 | 带电粒子在等效重力场中的运动 题目答案及解析
稿件来源:高途
高中 | 带电粒子在等效重力场中的运动题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
带电粒子在等效重力场中的运动
将一游戏装置放置在大小为$E=\dfrac{mg}{q}$,方向竖直向下的匀强电场中,该装置的轨道倾角$\theta$可以改变,当倾角为$30^\circ$时,质量为$2m$、带电量为$q(q\gt0)$的绝缘物块$A$恰好能沿着轨道匀速下滑。现将倾角调为$60^\circ$,使物块$A$从某高处由静止下滑,一段时间后物块$A$无碰撞地进入光滑水平面,与质量为$m$、带电量也为$q(q\gt0)$的绝缘物块$B$($B$被一根绳子悬挂,与水平面接触但不挤压)发生弹性正碰,碰后$A$、$B$各自的电量不变且$B$恰好能做完整的圆周运动,已知绳长为$L$,取重力加速度大小为$g$。求:
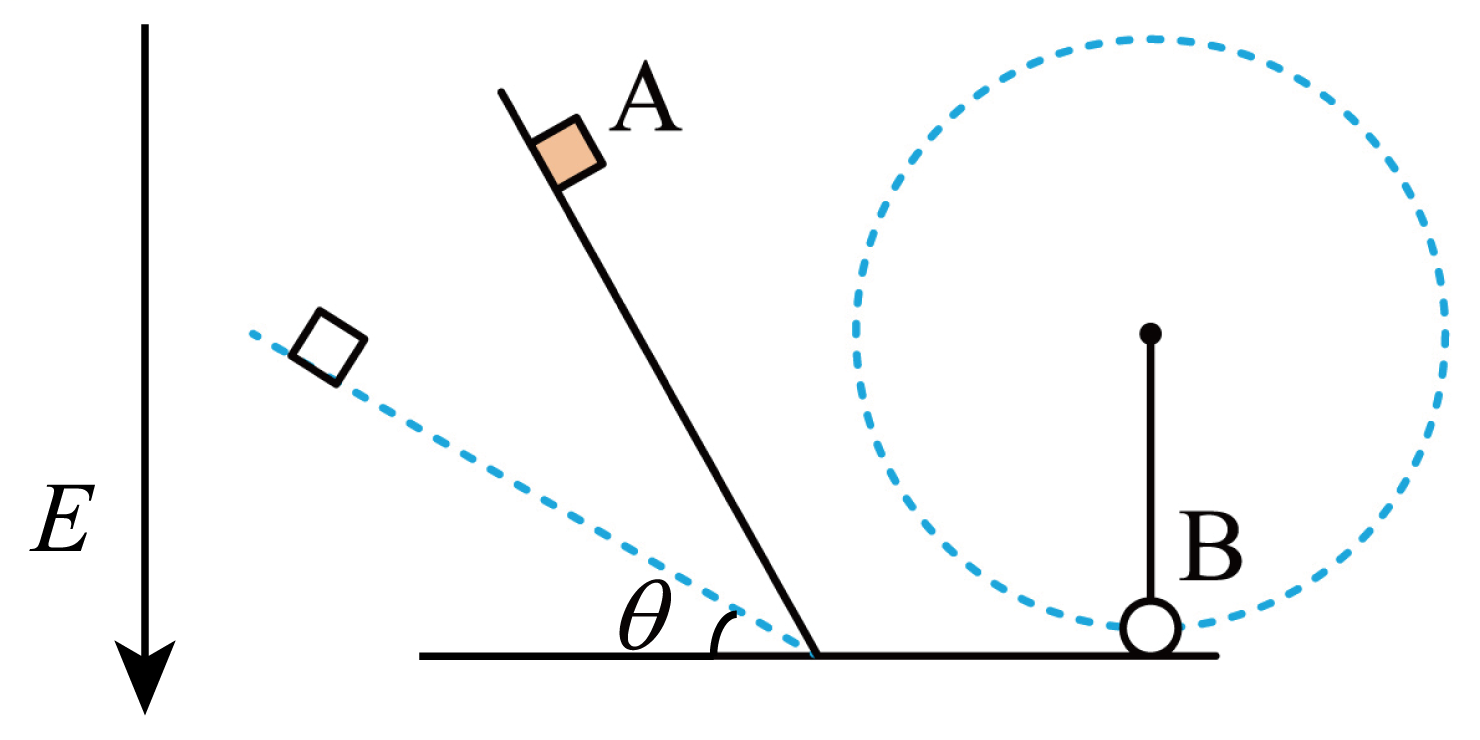
$A$与轨道间的动摩擦因数$\mu $;
$\\dfrac{\\sqrt{3}}{3}$
"]]当倾角为$30^\circ$时,$A$恰好能匀速下滑,对$A$受力分析可得$(2mg+qE)\sin 30^\circ=\mu (2mg+qE)\cos 30^\circ $
解得$\mu=\dfrac{\sqrt{3}}{3}$
碰前瞬间$A$的速度$v_{0}$。
$\\dfrac{3\\sqrt{10gL}}{4}$
"]]$A$、$B$发生弹性正碰,根据动量守恒有$2mv_{0}=2mv_{A}+mv_{B}$
根据机械能守恒有$\dfrac{1}{2} \times 2mv_{0}^{2}=\dfrac{1}{2} \times 2mv_{\text{A}}^{2}+\dfrac{1}{2}mv_{\text{B}}^{2}$
$B$在最高点,由牛顿第二定律得$mg+qE=\dfrac{mv^{2}}{L}$
$B$从最低点运动到最高点,由动能定理得$- 2(mg+qE)L=\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{\text{B}}^{2}$
联立解得$v_{0}=\dfrac{3\sqrt{10gL}}{4}$
高中 | 带电粒子在等效重力场中的运动题目答案及解析(完整版)
