高中 | 斜面问题 题目答案及解析
稿件来源:高途
高中 | 斜面问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
斜面问题
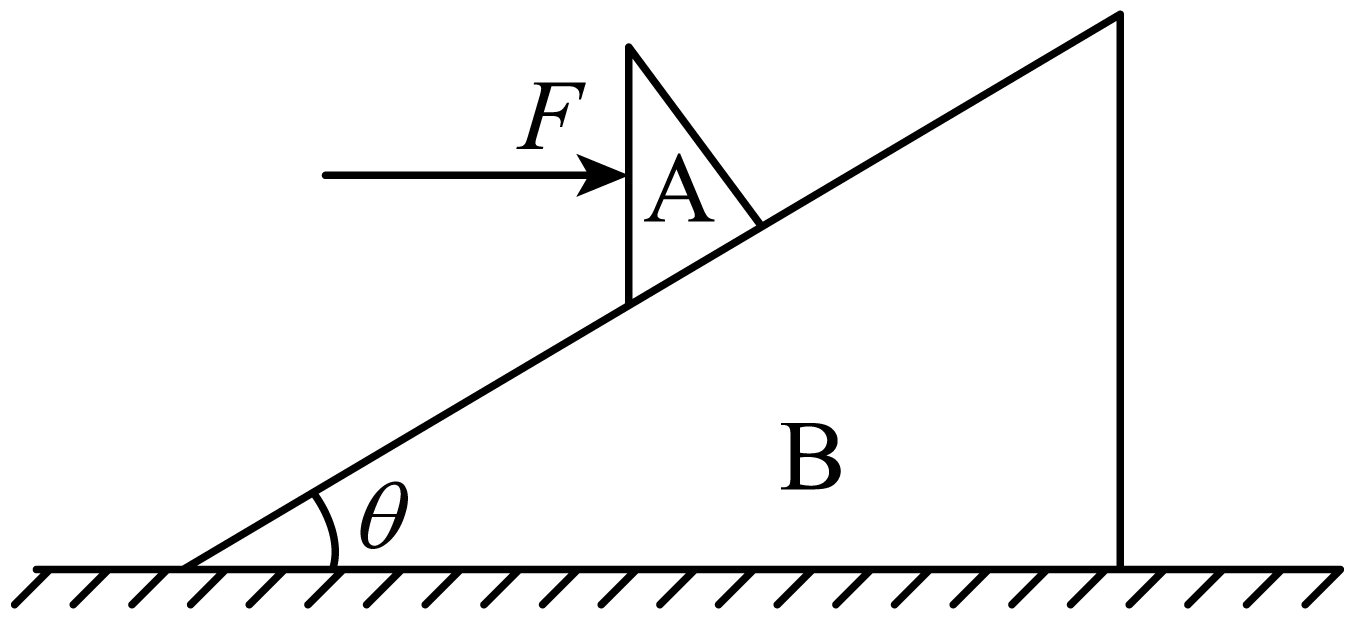
如图所示,质量为$m$的三角形木楔$A$,置于静止在水平面上的斜面体$B$上,斜面体$B$倾角为$\theta$,$A$与$B$之间的动摩擦因数为$\mu $,一水平力$F$作用在木楔$A$的竖直面上,在力$F$的推动下,木楔$A$沿斜面以恒定的加速度$a$向上滑动,此时斜面体$B$仍静止,则$(\qquad)$
$F$的大小为$\\dfrac{m\\left( a-g\\sin\\theta \\right)}{\\left( \\cos\\theta+\\mu\\sin\\theta \\right)}$
","$F$的大小为$\\dfrac{m\\left\\lbrack a+g\\left( \\sin\\theta+\\mu\\cos\\theta \\right) \\right\\rbrack}{\\cos\\theta-\\mu\\sin\\theta}$
","若增大$F$,方向不变,斜面体$B$一定仍保持静止
","若增大$F$,方向不变,斜面体$B$将可能向右运动
"]$\rm AB$.根据牛顿第二定律,对三角形木楔$A$受力分析,共受四个力$F$、$mg$、$F_{N}$、$f$,对力正交分解,垂直于斜面方向有$F_{N}=mg\cos \theta+F\sin \theta$
平行于斜面方向有$F\cos \theta-f - mg\sin \theta=ma$
斜面对木楔的摩擦力$f=\mu F_{N}$
联立解得$F=\dfrac{m\left\lbrack a+g\left( \sin\theta+\mu\cos\theta \right) \right\rbrack}{\cos\theta-\mu\sin\theta}$
故$\rm A$错误、$\rm B$正确;
$\rm CD$.对斜面受力分析,斜面受五个力,重力$G$,地面支持力$F_{1}$、地面的摩擦力$f_{地}$、木楔对斜面的压力$F_{N}{^\prime}$、木楔对斜面的摩擦力$f{^\prime}$,若增大$F$,方向不变,会导致$F_{N}{^\prime}$和$f{^\prime}$增大,进而导致水平方向合力增大,当超过最大静摩擦力时,斜面$B$会向右运动,故$\rm C$错误,故$\rm D$正确。
故选:$\rm BD$。
高中 | 斜面问题题目答案及解析(完整版)
