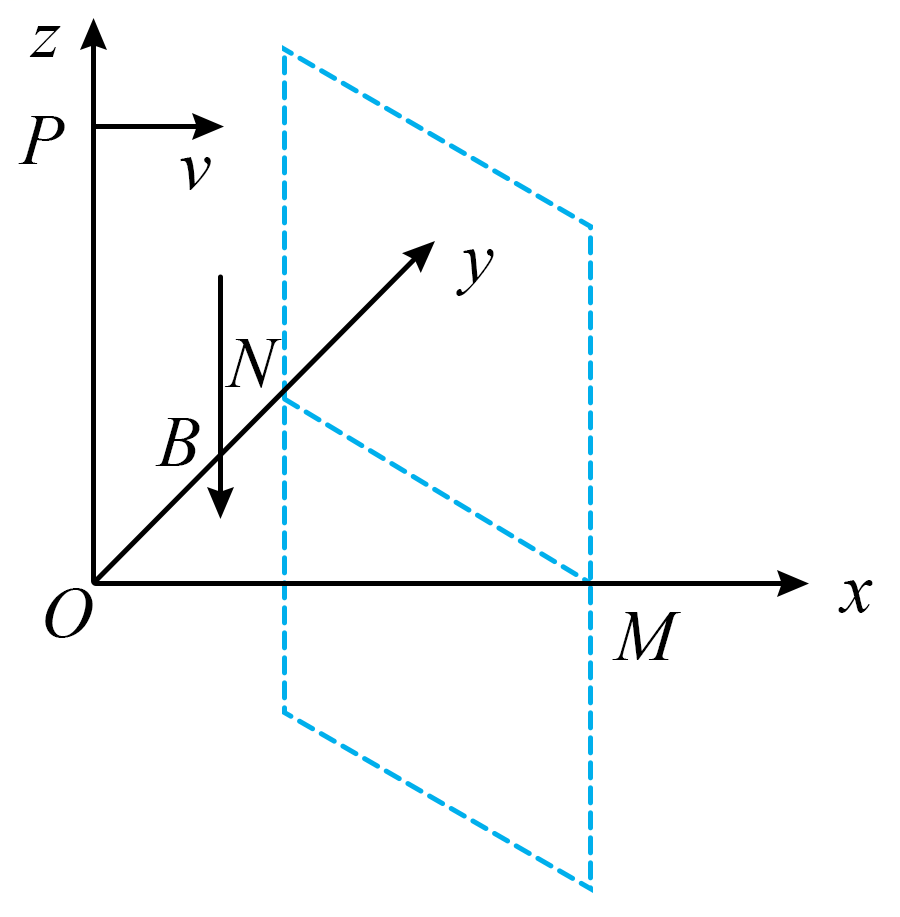
求粒子初速度的大小；

$\\dfrac{qBL}{m}$

粒子在与$xOy$平面平行的平面内做匀速圆周运动，半径$R=L$

由$qvB=\dfrac{mv^{2}}{R}$

解得$v_{0}=\dfrac{qBL}{m}$

若在空间中施加沿$z$轴负方向的匀强电场，恰好使粒子第二次与挡板碰撞发生在$xoy$平面，求匀强电场$E$的大小，并求出粒子第二次与挡板发生碰撞的空间坐标；

$\\dfrac{32qLB^{2}}{25\\pi^{2}m}$，$\\left( \\dfrac{3\\sqrt{2}}{2}L,\\left( 1- \\dfrac{3\\sqrt{2}}{2} \\right)L,0 \\right)$；

在与$z$轴垂直方向，发生第二次碰撞，经历时间为$t=\dfrac{5}{8}T$

其中$T$为粒子在磁场中匀速圆周运动的周期$T=\dfrac{2\pi m}{qB}$

在沿$z$轴方向，粒子做匀加速直线运动，由$\dfrac{1}{2}at^{2}=L$

根据牛顿第二定律$qE=ma$

联立得$E=\dfrac{32qLB^{2}}{25\pi^{2}m}$

粒子横坐标$x_{2}=3L\sin 45^\circ $

横坐标$y_{2}=L-3L\cos 45^\circ $

竖坐标$z_{2}=0$

粒子第二次与挡板发生碰撞的空间坐标为$\left( \dfrac{3\sqrt{2}}{2}L,\left( 1-\dfrac{3\sqrt{2}}{2} \right)L,0 \right)$。

在（$2$）的条件下，求粒子第$n$次与挡板碰撞的坐标。

答案见解析

在$x$轴方向，$n=1$时$x_{1}=\dfrac{\sqrt{2}}{2}L$

$n=2$时$x_{2}=\dfrac{3\sqrt{2}}{2}L$

$\cdots\cdots$

$x_{n}=\left( \sqrt{2}n-\dfrac{\sqrt{2}}{2} \right)L$

在$y$轴方向，$n=1$时$y_{1}=\left( 1-\dfrac{\sqrt{2}}{2} \right)L$

$n=2$时$y_{2}=\left( 1-\dfrac{3\sqrt{2}}{2} \right)L$

$\cdots\cdots$

$y_{n}=\left( \dfrac{2+\sqrt{2}}{2}-\sqrt{2}n \right)L$

在$z$轴方向，粒子做匀加速直线运动，不妨设粒子在与$z$轴垂直方向每次经过八分之一个同周运动时间为$t_{0}$，则$\dfrac{1}{2}a\left( 5t_{0} \right)^{2}=L$

$n=1$时

$z_{1}=L-\dfrac{1}{2}at_{0}^{2}=\dfrac{24}{25}L$

$n=2$时

$z_{2}=L-\dfrac{1}{2}a\left( 5t_{0} \right)^{2}=0$

$n=3$时$z_{3}=L-\dfrac{1}{2}a\left( 9t_{0} \right)^{2}=-\dfrac{56}{25}L$

$\cdots\cdots$

$z_{n}=\dfrac{- 16n^{2}+24n+16}{25}L$

粒子第$n$次与挡板碰撞的坐标为

$\left( \left( \sqrt{2}n-\dfrac{\sqrt{2}}{2} \right)L,\left( \dfrac{2+\sqrt{2}}{2}-\sqrt{2}n \right)L,\dfrac{- 16n^{2}+24n+16}{25}L \right)$，$n=1, 2, 3, 4\cdots\cdots$