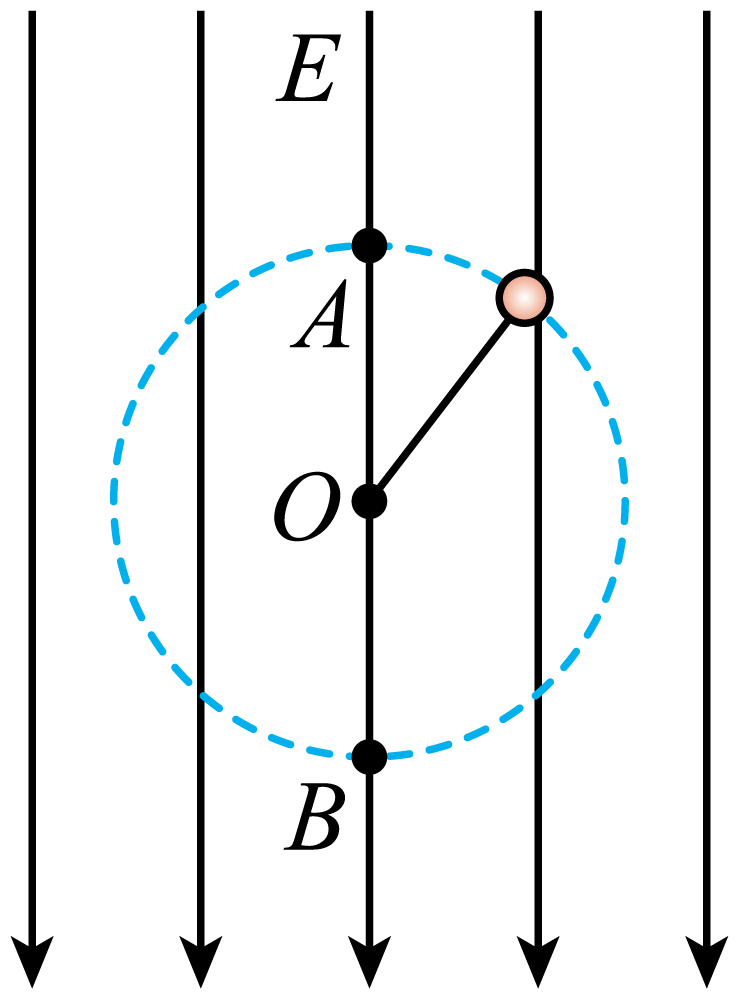
如图所示，场强为$E$的匀强电场方向竖直向下，所带电荷量为$-q$，质量为$m$的带电小球用长为$L$的绝缘细线拴住，小球可以在竖直平面内绕О做圆周运动，$A$、$B$分别是轨迹的最高点和最低点。已知小球静止时的位置是$A$点，重力加速度大小为$g$，小球可以看成质点，下列说法正确的是$(\qquad)$

若小球静止在$A$点时给球一垂直绳的极小速度，则小球经$\\pi\\sqrt{\\dfrac{mL}{qE-mg}}$再次回到$A$点

若小球静止在$A$点时给球一垂直绳的极小速度，则小球经$\\pi\\sqrt{\\dfrac{mL}{qE}}$再次回到$A$点

若小球恰好可以做完整的圆周运动，则小球通过$A$点时速度最小值为$\\pi\\sqrt{\\dfrac{5qEL}{m}}$

若小球恰好可以做完整的圆周运动，则小球通过$A$点时速度最小值为$v_{A}=\\sqrt{\\dfrac{5(qE-mg)L}{m}}$

$\rm AB$．小球在复合场中做简谐振动，对其受力分析可知$qE−mg=mg'$

解得$g'=\dfrac{qE-mg}{m}$

将小球的简谐振动类比于单摆，可知其振动周期$T=2\pi\sqrt{\dfrac{L}{g'}}=2\pi\sqrt{\dfrac{mL}{qE-mg}}$

小球再次回到$A$点时需半个周期的时间，即$t=\dfrac{1}{2}T=\pi\sqrt{\dfrac{mL}{qE-mg}}$

$\rm A$正确，$\rm B$错误；

$\rm CD$．设小球在$B$点的速度为$v_{B}$，则有$qE-mg=m\dfrac{v_{B}^{2}}{L}$

根据动能定理可得$(qE-mg) \cdot 2L=\dfrac{1}{2}mv_{A}^{2}-\dfrac{1}{2}mv_{B}^{2}$

联立上述各式解得$v_{A}=\sqrt{\dfrac{5(qE-mg)L}{m}}$

故$\rm C$错误，$\rm D$正确。

故选：$\rm AD$。