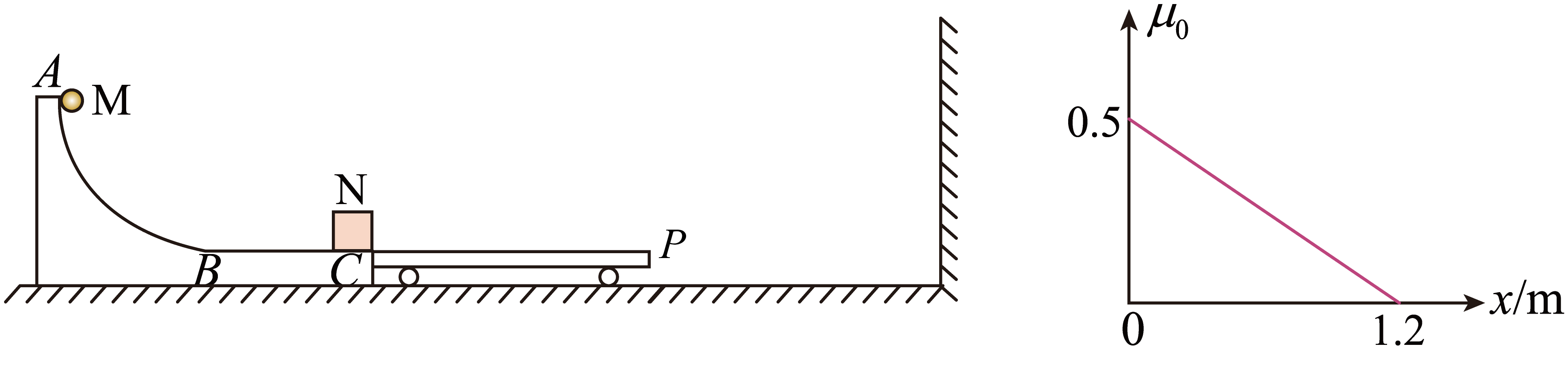
圆弧半径$R$的大小；

$7.5\\ \\rm m$

根据题意，由$\mu _{0}-x$图像可知，小球$M$从$B$点到$C$点克服摩擦力做功为$W_{{f}}=\dfrac{1}{2}\mu_{0}Lm_{2}g=6\;\rm \text{J}$

小球$M$从斜槽顶端$A$点运动到$C$点过程中，由动能定理有$m_{2}gR-W_{{f}}=\dfrac{1}{2}m_{2}v_{0}^{2}$

解得$R=7.5\ \rm m$；

小车与墙壁第$1$次碰撞后到与墙壁第$2$次碰撞前瞬间的过程中，滑块与小车间由于摩擦产生的热量；

$48\\;\\rm J$

根据题意，在$C$点，小球$M$与滑块$N$发生弹性碰撞，由动量守恒定律和能量守恒定律有$m_{2}v_{0}=m_{2}v'_{2}+m_{1}v$

$\dfrac{1}{2}m_{2}v_{0}^{2}=\dfrac{1}{2}m_{2}{v'}_{2}^{2}+\dfrac{1}{2}m_{1}v^{2}$

解得$v'_{2}=0$，$v=v_{0}=12\;\rm m/s$

可知，小球与滑块碰后小球静止，滑块以$12\ \text m/s$的速度滑上小车，由于小车右端距离墙壁足够远，小车足够长，则滑块滑上后，小车与墙壁第$1$次碰撞前，滑块和小车一定达到共同速度，设为$v_{1}$，由动量守恒有$m_{1}v=(m_{1}+m_{0})v_{1}$

解得$v_{1}=8\;\rm m/s$

小车与墙壁第$1$次碰撞后小车速度变为$-\dfrac{1}{2}v_{1}$，滑块速度仍为$v_{1}$，碰后达到共同速度为$v_{2}$，由动量守恒定律有$- \dfrac{1}{2}m_{0}v_{1}+m_{1}v_{1}=\left( m_{1}+m_{0} \right)v_{2}$

解得$v_{2}=4\;\rm m/s$

小车与墙壁第$1$次碰撞后到与墙壁第$2$次碰撞前过程中，滑块与小车间产生的热量为$Q$，根据能量守恒得$\dfrac{1}{2}m_{0}\left( \dfrac{1}{2}v_{1} \right)^{2}+\dfrac{1}{2}m_{1}v_{1}^{2}=\dfrac{1}{2}\left( m_{1}+m_{0} \right)v_{2}^{2}+Q$

联立得$Q=48\;\rm J$；

小车与墙壁第$1$次碰撞后到与墙壁第$4$次碰撞前瞬间的过程中，小车运动的路程；

$10.5\\ \\rm m$

根据牛顿第二定律有，滑块与小车相对运动过程中加速度大小分别为

$a_{1}=\dfrac{\mu m_{1}g}{m_{1}}=1\ \rm m/\text{s}^{2}$，$a_{2}=\dfrac{\mu m_{1}g}{m_{3}}=2\;\rm \text{m/s}^{2}$

由（$2$）分析可知，小车第一次碰后的速度为$- \dfrac{v_{1}}{2}=- 4\dfrac{\text{m}}{\text{s}}$

小车和滑块再次共速时的速度为$v_{2}=4\ \text{m/s}$

小车向左减速到$0$的时间为$t_{1}=\dfrac{\dfrac{v_{1}}{2}}{a_{2}}=2\;\rm \text{s}$

向左运动的距离为$x_{1}=\dfrac{\dfrac{v_{1}}{2}}{2}t_{1}=4\;\rm \text{m}$

同理可得，小车向右加速到与滑块共速的时间为$t_{2}=\dfrac{v_{2}}{a_{2}}=2\;\rm \text{s}$

向右运动的距离为$x_{2}=\dfrac{v_{2}}{2}t_{2}=4\;\rm \text{m}$

则小车在第一次碰后到小车和滑块再次共速运动的位移为$0$，即滑块和小车在二次碰墙前恰好达到共速，分析可知，每次碰撞前两者恰好达到共同速度，则小车与墙壁第$1$次碰撞到第$2$次碰撞前过程中的路程为$s_{1}=x_{1}+x_{2}=8\ \rm m$

同理小车与墙壁第$2$次碰撞到第$3$次前碰撞过程中的路程为$s_{2}=2\ \rm m$

第$3$次碰撞到第$4$次碰撞前过程中的路程为$s_{3}=0.5\ \rm m$

则小车与墙壁第$1$次碰撞后到与墙壁第$4$次碰撞前瞬间的过程中，小车运动的路程为$s=s_{1}+s_{2}+s_{3}=10.5\ \rm m$；

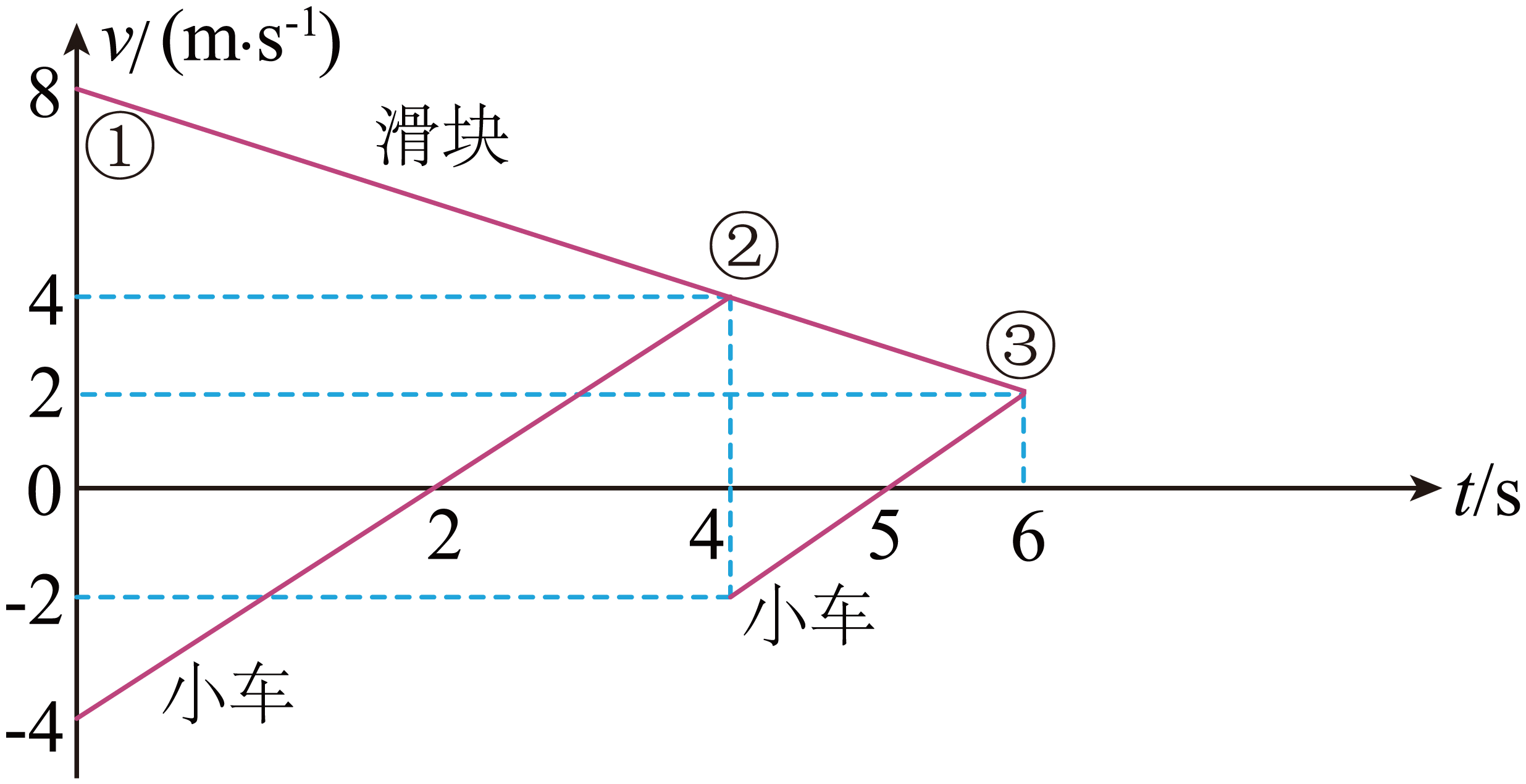
画出小车与墙壁前三次碰撞时间内小车和滑块的$v − t$图像，不要求推导过程。

答案见解析

综上所述，以小车第一次碰后为计时起点，画出小车与墙壁前三次碰撞时间内小车和滑块的$v-t$图像，如图所示：