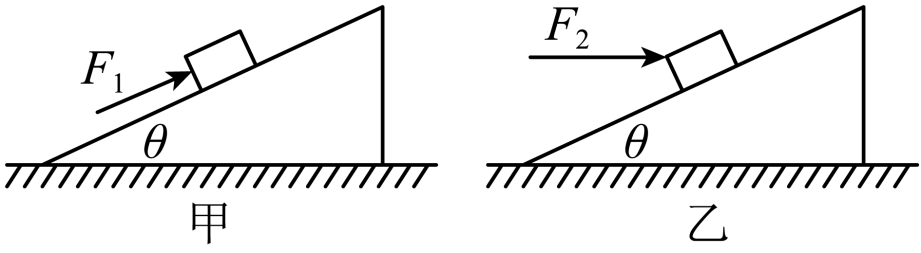
如图，质量为$m$的物体置于倾角为$\theta$的固定斜面上，物体与斜面之间的动摩擦因数为$\mu $，先用平行于斜面的推力$F_{1}$作用于物体上，使其能沿斜面匀速上滑，若改用水平推力$F_{2}$作用于物体上，也能使物体沿斜面匀速上滑，则两次力之比$\dfrac{F_{1}}{F_{2}}$为$(\qquad)$

$\\cos\\theta+\\mu \\sin\\theta$

$\\cos\\theta$–$\\mu \\sin\\theta$

$l+\\mu \\tan\\theta$

$1$–$\\mu \\tan\\theta$

$F_{1}$作用时，物体的受力情况如图$1$：

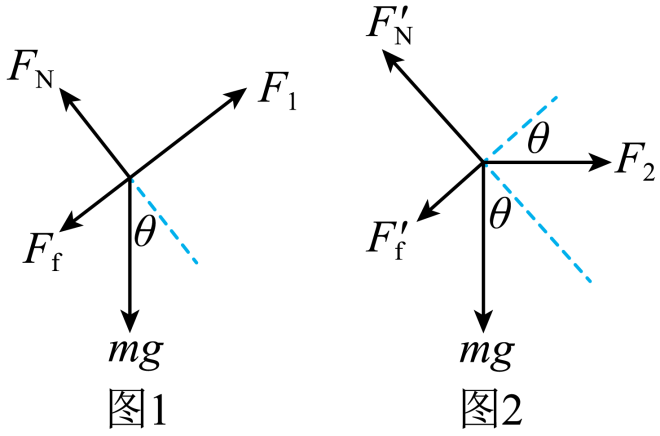
根据平衡条件得：$F_{1}=mg\sin\theta+\mu F_{N}$，$F_{N}=mg\cos\theta$

解得：$F_{1}=mg\sin\theta+\mu mg\cos\theta$

$F_{2}$作用时，物体的受力情况如图$2$，根据平衡条件得：$F_{2}\cos\theta=mg\sin\theta+\mu F_{N}^\prime$，$F_{N}^\prime=mg\cos\theta+F_{2}\sin\theta$

解得：$F_{2}=\dfrac{mg\sin\theta+\mu mg\cos\theta}{\cos\theta-\mu \sin\theta}$

所以$\dfrac{F_{1}}{F_{2}}=\dfrac{\begin{array}{r} mg\sin\theta+\mu mg\cos\theta \end{array}}{\dfrac{mg\sin\theta+\mu mg\cos\theta}{\cos\theta-\mu \sin\theta}}=\cos\theta-\mu \sin\theta$ 。

故选：$\rm B$。