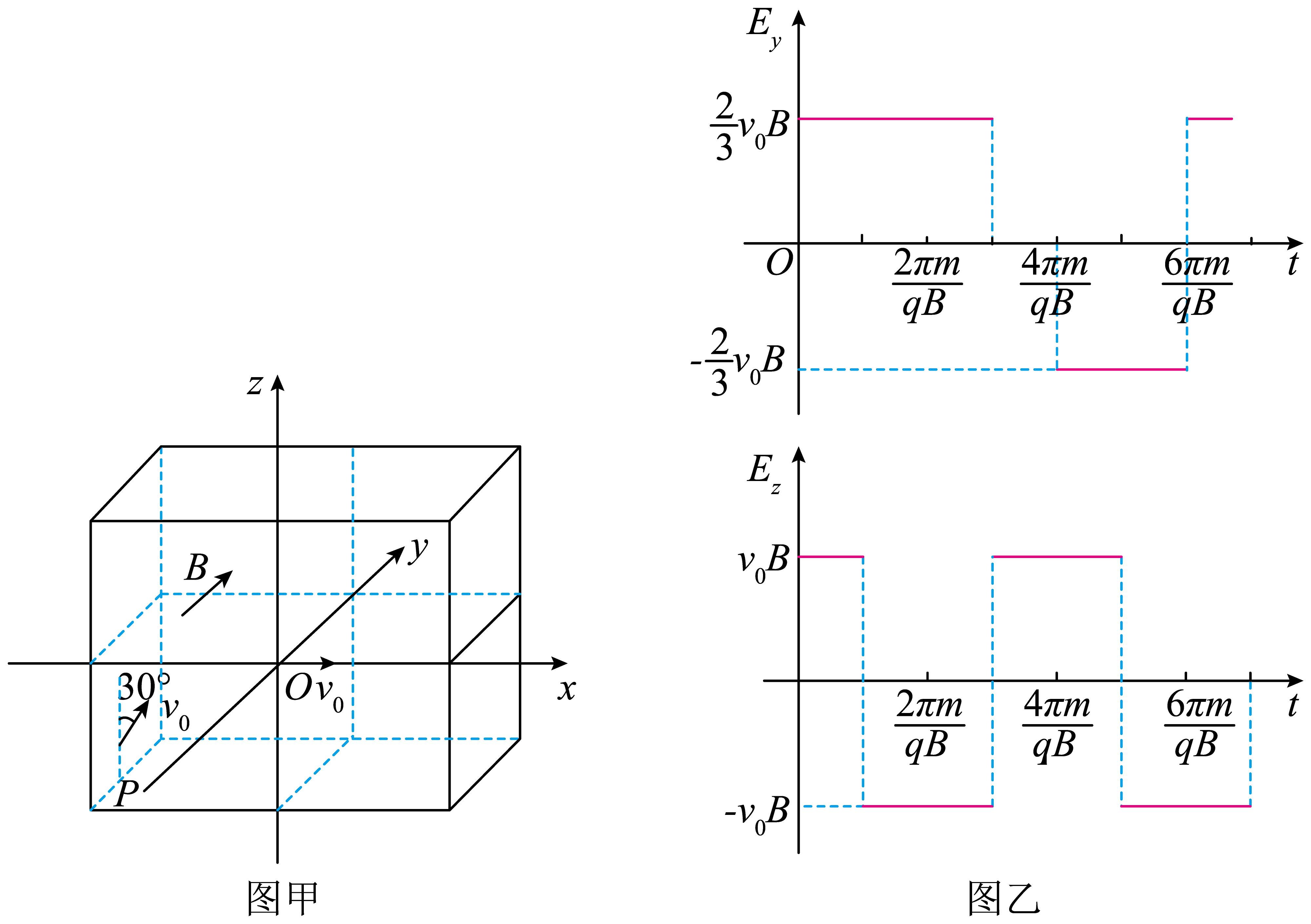
粒子源所在区域匀强电场的电场强度$E$；

$E= \\dfrac{3 m{v_{0}}^{2}}{4qd}$

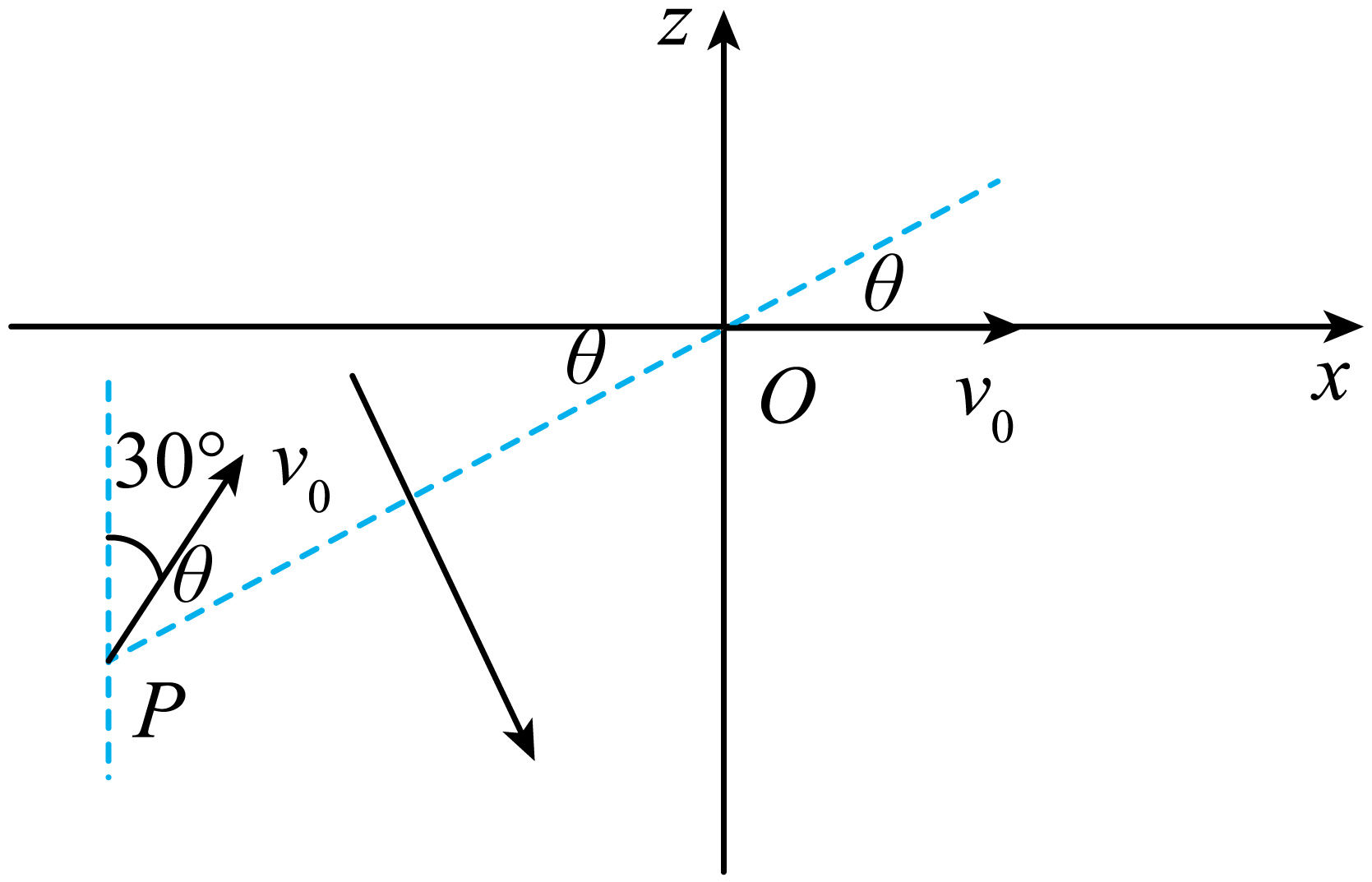
连结$OP$，由图可知$\theta=30^\circ$，电场强度$E$与$OP$垂直（或与$x$正方向夹$60^\circ$斜向右下）

$x$方向列牛顿第二定律$qE\cos 60^\circ =ma_{x}$

由运动学方程$2a_{x}d=v_{o}^{2}-(v_{o}\sin 30^\circ)^{2}$

得$E=\dfrac{3m{v_{0}}^{2}}{4qd}$；

当$t=\dfrac{\pi m}{qB}$时，粒子的速度大小$v$；

$v= \\sqrt{1+\\pi^{2}}\\cdot v_{0}$；

粒子在$xOz$平面内做匀速圆周运动，在时间$t=\dfrac{\pi m}{qB}$内，$z$轴方向无电场，$y$轴有电场，沿$y$轴方向匀加速直线运动$qE_{y}\cdot \dfrac{\pi m}{qB}=mv_{y}-0$

$v=\sqrt{{v_{0}}^{2}+{v_{y}}^{2}}=\sqrt{1+\pi^{2}}\cdot v_{0}$；

从计时开始，粒子第一次回到原点经历的时间$t_{0}$及满足轨迹约束的长方体磁场的最小体积$V$；

$\\dfrac{(8\\pi+12)\\pi^{2}}{3}\\left( \\dfrac{mv_{0}}{qB} \\right)^{3}$；

粒子在$xOz$平面内轨迹如图所示，

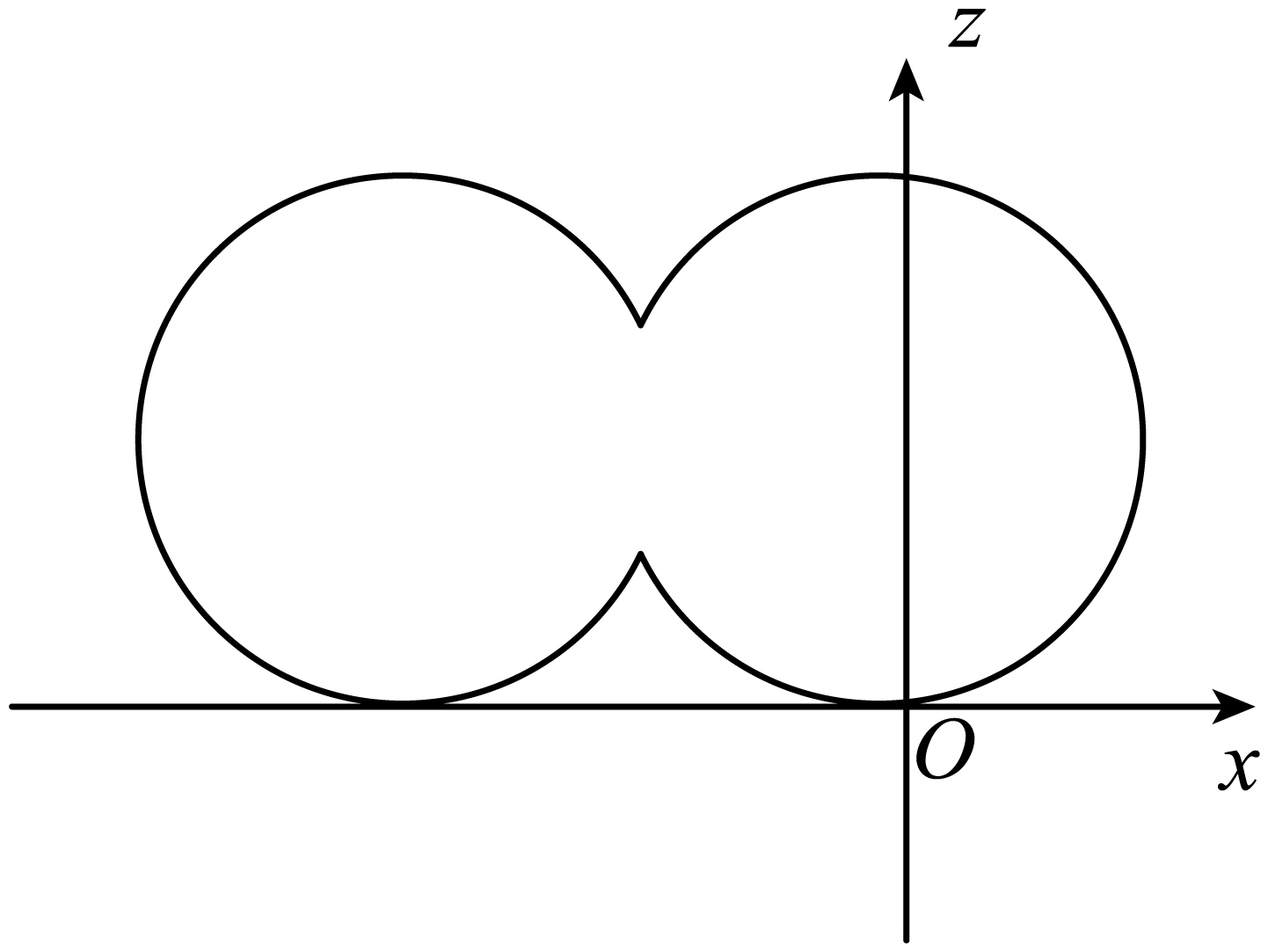
$0\sim\dfrac{\pi m}{qB}$，粒子做匀速圆周运动，$Bqv_{0}=m\dfrac{{v_{0}}^{2}}{r_{1}}$

$r_{1}=\dfrac{mv_{0}}{qB}$，$\dfrac{\pi m}{qB}\sim\dfrac{\text{3}\pi m}{qB}$，粒子作轮滚线运动，（当电场与部分磁场作用相抵消时）可视作沿$x$轴方向匀速直线运动和（以剩余的速度）$xOz$平面匀速圆周运动的叠加，匀速直线运动的速度为$Bqv_{1}=qE_{z}$，$v_{1}=\dfrac{2}{3}v_{0}$

一个周期内前进的距离和回到原点的时间分别为$x=v_{1}\dfrac{2\pi m}{qB}=\dfrac{4\pi m}{3qB}v_{0}$

$t_{xOz}=2\left(\dfrac{T}{2}+T\right) \times n=6n\dfrac{\pi m}{qB}(n=1,2,3\cdots\cdots)$

粒子在$y$轴方向作周期性的匀变速直线运动，其$v-t$图像如图所示，

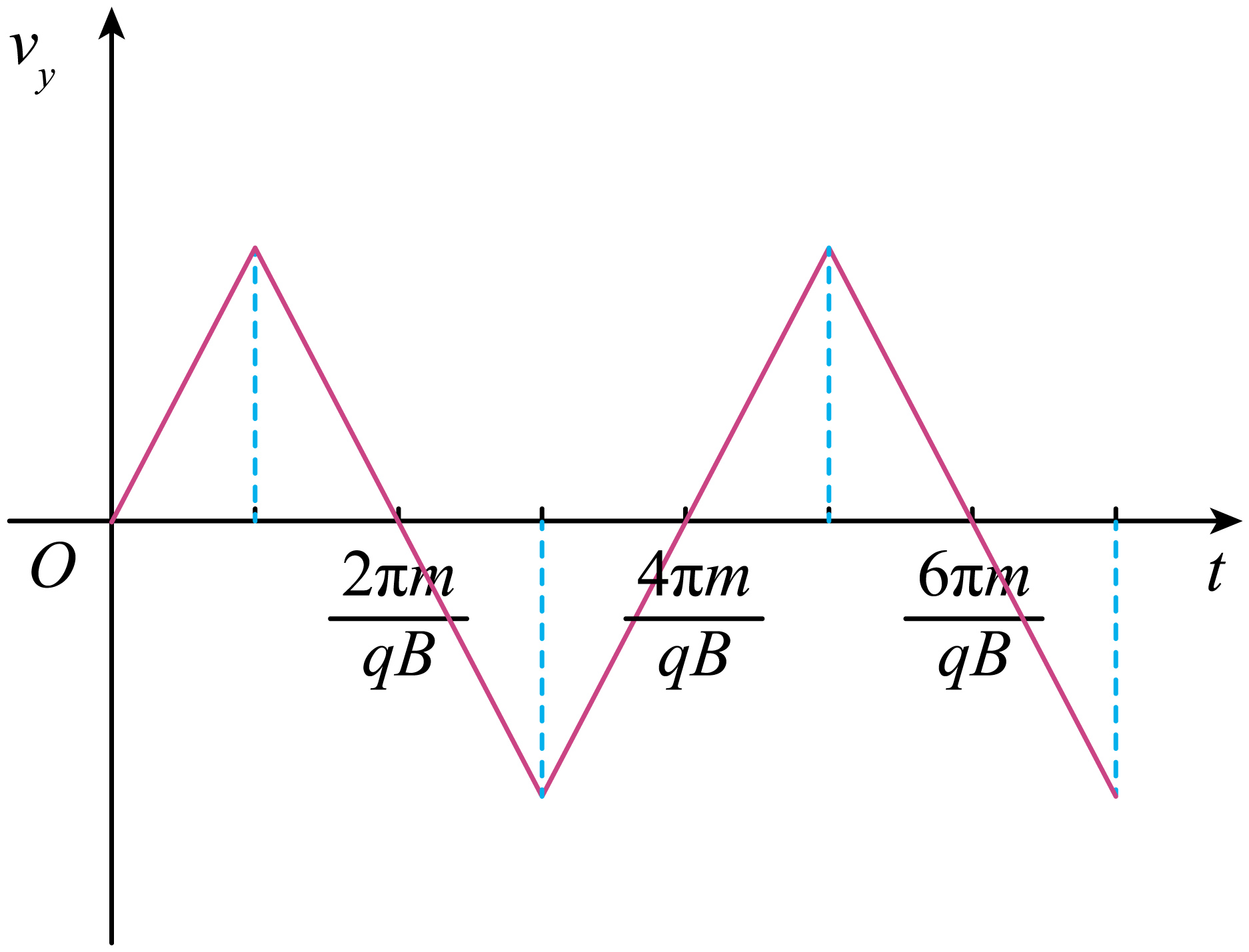
可知粒子往复运动，运动的最大距离和回到原点的时间分别为$y=2 \times \dfrac{1}{2}a_{y}t^{2}=\dfrac{\pi^{2}mv_{0}}{qB}$

$t_{y}=4kt=4k\dfrac{\pi m}{qB}(k=1,2,3\cdots\cdots)$

则回到原点，应为$xoz$平面运动和$y$轴运动回到原点的时间的公倍数$t_{0}=\dfrac{12n\pi m}{qB}(n=1,2,3\cdots\cdots)$

当$n=1$时，第一次回到原点

$t_{0}=\dfrac{12\pi m}{qB}$

$x$轴长度为$2r_{1}+x$，$y$轴长度为上面式中的$y$，$z$轴长度为$2r_{1}$，所以限制约束的最小体积为$V=2r_{1}\times (2r_{1}+x) \times y=\dfrac{(8\pi+12)\pi^{2}}{3}\left( \dfrac{mv_{0}}{qB} \right)^{3}$；

在（$3$）的时间内，粒子有可能发生碰撞的点有几个？（含原点，不需要写出过程）

$4$。

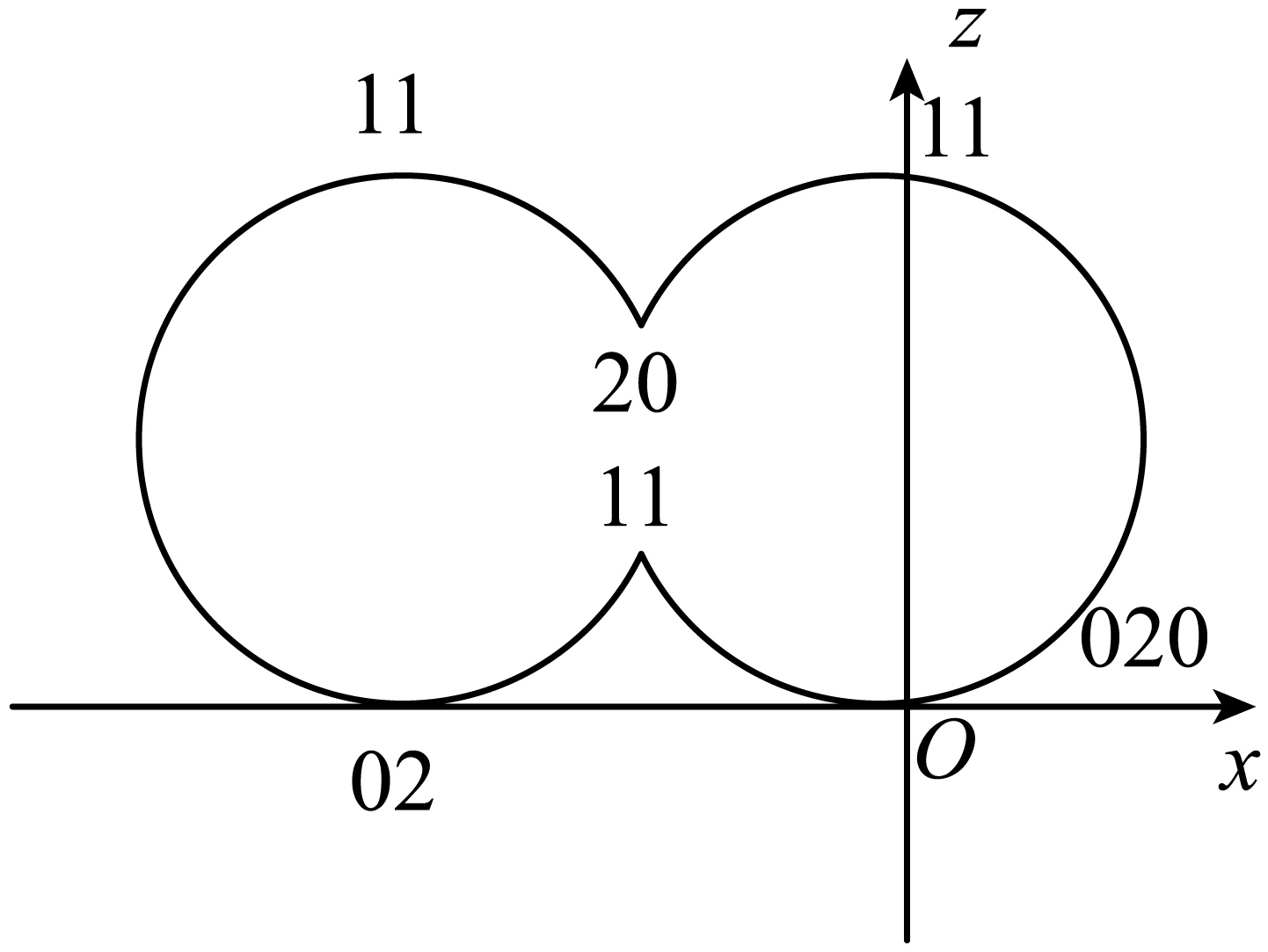
$4$次（注意空间感觉的想像，将下图在$y$轴上的情况要想像进去，主要看$y$轴方向上的碰撞）从图中的$11$到$20$到$11$的上半过程可能由两次碰撞，对称的下面有两次碰撞。（点附近的数字表示$y$方向上的移动距离，$1$表示$0.5y$）。