高中 | 动量守恒之木板滑块模型 题目答案及解析
稿件来源:高途
高中 | 动量守恒之木板滑块模型题目答案及解析如下,仅供参考!
选修3-5
第十六章 动量守恒定律
16.3 动量守恒定律
动量守恒之木板滑块模型
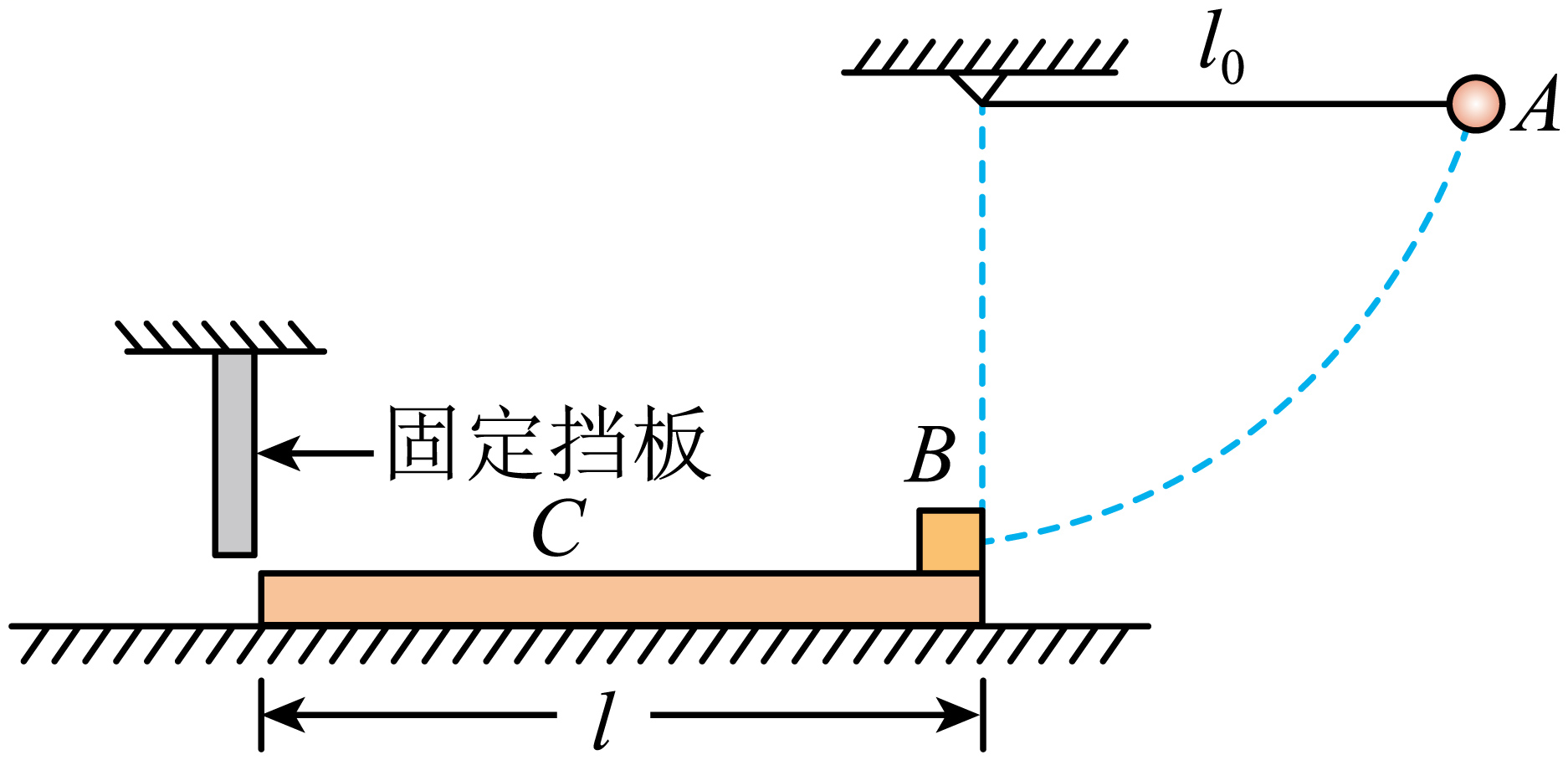
如图所示,质量$M=3\;\rm kg$,长度$l=3.75\;\rm m$的木板$C$置于光滑水平地面上,质量$m=1\;\rm kg$的物块$B$放在木板$C$的右端,在木板$C$左端正上方固定一弹性挡板,挡板与地面的距离正好能使木板$C$通过。一长度$l_{0}=4.05\;\rm m$不可伸长的轻绳一端固定,另一端连接质量$m_{0}=0.5\;\rm kg$的小球$A$,将小球$A$拉至水平并由静止释放,轻绳竖直时小球$A$刚好与物块$B$碰撞,物块$B$与小球$A$及挡板的碰撞均为弹性碰撞。将物块$B$与小球$A$视为质点,运动过程不计空气阻力,已知物块$B$与木板$C$间的动摩擦因数$\mu =0.5$,重力加速度$g$取$10\;\rm m/s^{2}$。求:
小球$A$与物块$B$碰撞后轻绳与竖直方向的最大角度为$\theta$,计算$\cos\theta$的值;
$\\dfrac{8}{9}$;
"]]对小球$A$机械能守恒$m_{0}gl_{0}=\dfrac{1}{2}m_{0}{v_{0}}^{2}$
$v_{0}=9\;\rm m/s$
弹性碰撞动量和能量关系$m_{0}v_{0}=m_{0}v'+mv_{1}$
$\dfrac{1}{2}m_{0}{v_{0}}^{2}=\dfrac{1}{2}m_{0}v'^{2}+\dfrac{1}{2}m{v_{1}}^{2}$
解得$v'=-3\;\rm m/s$,$v_{1}=6\;\rm m/s$
对小球$A$碰撞后机械能守恒$\dfrac{1}{2}m_{0}v'^{2}=m_{0}gh$
$\cos\theta=\dfrac{l_{0}-h}{l_{0}}=\dfrac{8}{9}$;
物块$B$与木板$C$左端的最小距离;
$1.05\\;\\rm m$;
"]]$B$在$C$上滑动过程$\mu mg=ma_{B1}$
$a_{B1}=5\;\rm m/s^{2}$
$\mu mg=Ma_{C1}$
$a_{C1}=\dfrac{5}{3}\ \text{m/s}^{2}$
假设$BC$共速后,$B$与挡板碰撞,有$v_{1}-a_{B1}t_{1}=a_{C1}t_{1}$
$v=v_{1}-a_{B1}t_{1}=1.5\;\rm m/s$
$t_{1}=0.9\;\rm s$
$s_{B1}=3.375\;{\rm m}\lt l$
假设成立。$s_{C1}=0.675\;\rm m$
$\Delta s_{1}=s_{B1}-s_{C1}=2.7\;\rm m$
$l_{1}=l-\Delta s_{1}=1.05\;\rm m$;
物块$B$与挡板前两次碰撞的时间间隔;
$0.675\\;\\rm s$;
"]]第一次碰后$v_{C}=1.5\;\rm m/s$
$v_{B}=-1.5\;\rm m/s$
$v_{C}-a_{C1}t_{2}=v_{B}+a_{B1}t_{2}$
$t_{2}=0.45\;\rm s$
$s_{B2}=- \dfrac{27}{160}\ \text{m}$
$v_{2}=v_{C}-a_{C1}t_{2}=0.75\;\rm m/s$
$t_{3}=-\dfrac{s_{B2}}{v_{2}}=0.225\;\rm \text{s}$
$\Delta t=t_{2}+t_{3}=0.675\;\rm s$;
最终物块$B$与木板$C$右端的距离。
$1.8\\;\\rm m$。
"]]与挡板碰撞后$\Delta s_{2}=0.675\;\rm m$
$\Delta s_{3}=\dfrac{1}{4}\Delta s_{2}$
碰后$B$相对于$C$向右的总位移$\Delta s=\Delta s_{2}+\Delta s_{3}+\cdots+\Delta s_{n}=0.9\;\rm m$
则$l_{右}=\Delta s_{1}-\Delta s=1.8\;\rm m$。
高中 | 动量守恒之木板滑块模型题目答案及解析(完整版)
