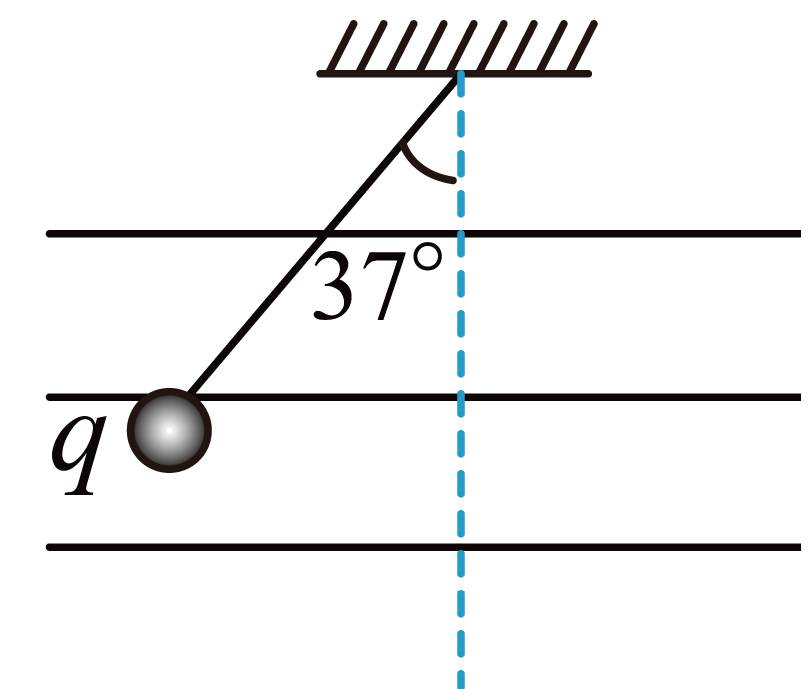
匀强电场的电场强度$E$大小和方向；

$\\dfrac{3mg}{4q}$，水平向左；

小球在电场中静止时根据共点力平衡得$qE=mg\tan 37^\circ $

则$E=\dfrac{mg\tan 37^\circ }{q}=\dfrac{3mg}{4q}$

方向水平向左；

若将原电场方向改为竖直向上，大小保持不变，则小球从图示位置由静止释放瞬间绳子的拉力大小；

$\\dfrac{1}{5}mg$；

若将原电场方向改为竖直向上时小球释放的瞬间向心力为零，根据牛顿第二定律得$T=(mg-qE)\cos 37^\circ =\dfrac{1}{5}mg$

若将原电场方向改为竖直向上，大小保持不变，则小球从图示位置由静止释放后运动过程中细线的最大拉力大小  

$\\dfrac{7}{20}mg$

根据小球的运动情况可知小球在最低点时拉力最大，小球从图示位置到最低点处根据动能定理得$(mg-qE)l(1-\cos 37^\circ )=\dfrac{1}{2}mv^{2}$

在最低点处$T+qE-mg=\dfrac{mv^{2}}{l}$

故细线所受得最大拉力为$\dfrac{7}{20}mg$。