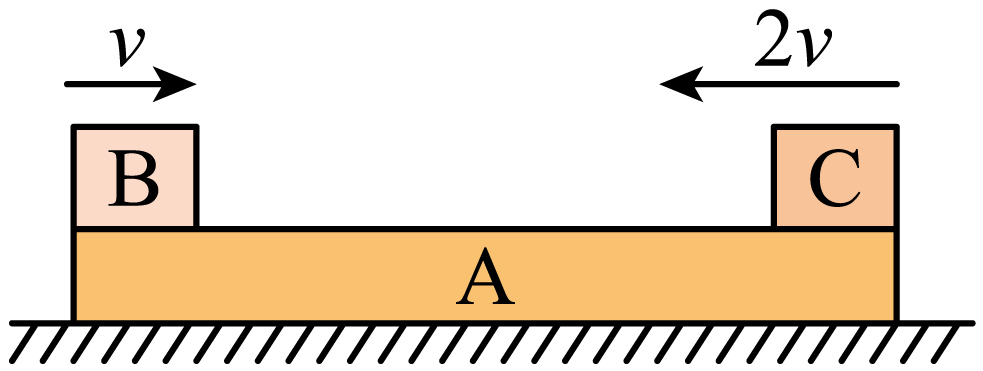
$B$、$C$刚滑上长木板$A$时，$A$所受合外力为多大？

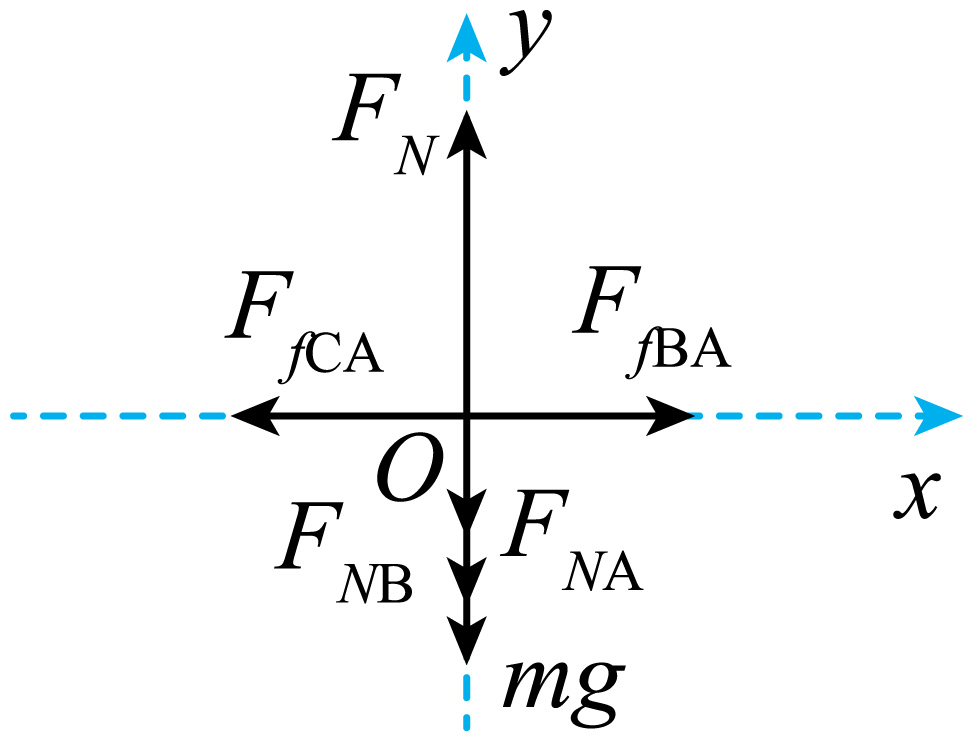
$F_{A合}=0$；

对$A$受力分析可知，$A$在竖直方向上受力平衡，在水平方向上因物块$B$、$C$与长木板$A$间的动摩擦因数均为$\mu $，$B$、$C$质量相等，故$F_{fCA}=F_{fBA}$，即$F_{A合}=0$；

长木板$A$的最终运动速度为多大？

$\\dfrac{v}{3}$；

$A$、$B$、$C$组成的系统动量守恒，规定向左方向为正方向，由动量守恒定律有：$2mv-mv=3mv'$

解得$A$、$B$、$C$最终的共同速度$v'=\dfrac{v}{3}$，即木板$A$最终运动的速度为$\dfrac{v}{3}$；

为使物块$B$、$C$不相撞，长木板$A$至少多长？

$\\dfrac{7v^{2}}{3\\mu g}$。

由能量转化与守恒定律有：$Q_{总}=\dfrac{1}{2}mv^{2}+\dfrac{1}{2}m{(2v)}^{2}-\dfrac{1}{2} \cdot 3m\left( v'\right)^{2}$

$Q_{总}=\mu mg\cdot(\Delta x_{BA}+\Delta x_{CA}+\Delta x_{CA}')=\mu mg\Delta x_{总}$

为使$B$、$C$不相撞由题意分析可知$l_{A}\geqslant \Delta x_{总}$

解得：$l_{A} \geqslant \dfrac{7v^{2}}{3\mu g}$

即长木板$A$的最小长度为$\dfrac{7v^{2}}{3\mu g}$。