高中 | 动量守恒之木板滑块模型 题目答案及解析
稿件来源:高途
高中 | 动量守恒之木板滑块模型题目答案及解析如下,仅供参考!
选修3-5
第十六章 动量守恒定律
16.3 动量守恒定律
动量守恒之木板滑块模型
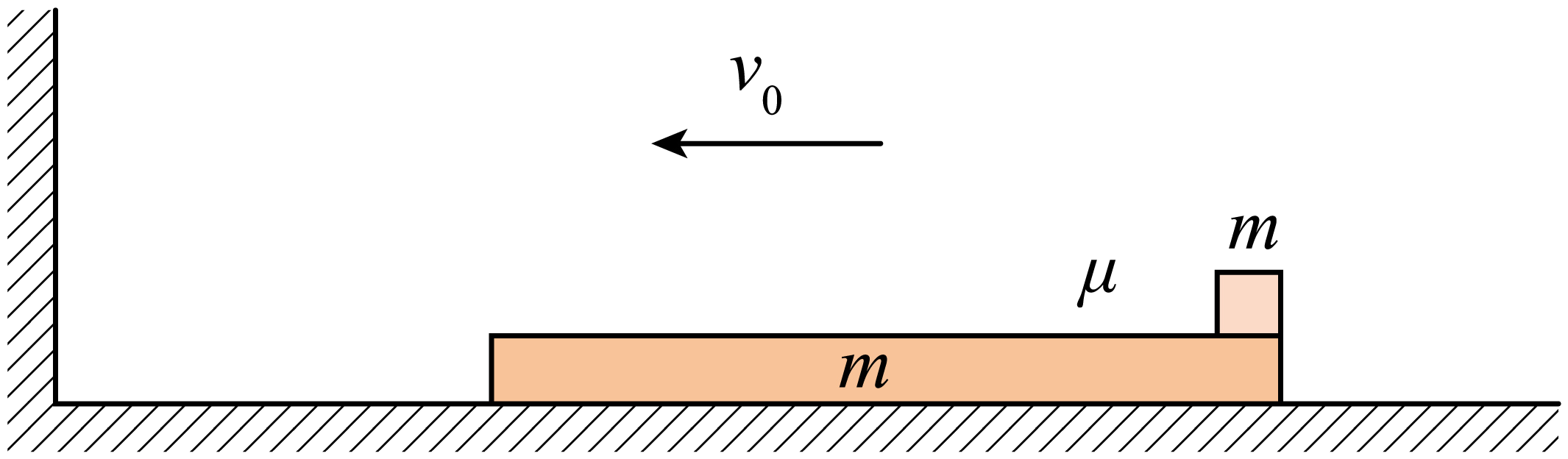
如图所示,光滑水平面上有一质量为$m=1\;\rm kg$、长度为$L$的长木板,其右端有一质量为$m=1\;\rm kg$的滑块(可视为质点),滑块与木板间动摩擦因数为$\mu =0.5$。初始时,二者以共同的速度$v_{0}=4\;\rm m/s$一起向左运动,木板每次与墙面碰撞后瞬间,速度大小变为原来的一半,并反向运动。整个过程,滑块既没有从木板上掉下,也没有与墙面发生接触。知重力加速度$g$取$10\;\rm m/s^{2}$,求:
首次碰撞后开始计时,木板速度第一次减为零时的位移大小;
$0.4\\;\\rm m$;
"]]第$1$次碰撞后,木板向右做匀减速直线运动,速度为零时,位移为$s$
对木板由动能定理可得$- \mu mgs=- \dfrac{1}{2}m\left( \dfrac{v_{0}}{2} \right)^{2}$
解得$s=\dfrac{v_{0}^{2}}{8\mu g}$
代入数据得$s=0.4\;\rm m$;
木板长度$L$的最小值;
$1.92\\;\\rm m$;
"]]之后,木板向左做匀加速直线运动,设板块最终有共同速度$v_{1}$,对于系统,由动量守恒定律得$mv_{0}-m\dfrac{v_{0}}{2}=2mv_{1}$
解得$v_{1}=\dfrac{v_{0}}{4}$
即板块以共同的速度$\dfrac{v_{0}}{4}$再次与墙面发生二次碰撞,第$1$次碰撞后至第$1$次共速二者相对位移为$L_{1}$,由能量守恒$\mu mgL_{1}=\dfrac{1}{2}mv_{0}^{2}+\dfrac{1}{2}m\left( \dfrac{v_{0}}{2} \right)^{2}-\dfrac{1}{2} \cdot 2m\left( \dfrac{v_{0}}{4} \right)^{2}$
解得$L_{1}=\dfrac{9v_{0}^{2}}{16\mu g}$
同理$m\dfrac{v_{0}}{4}-m\dfrac{v_{0}}{8}=2mv_{2}$
解得$v_{2}=\dfrac{v_{0}}{16}=\dfrac{v_{0}}{4^{2}}$
第$2$次碰撞后至第$2$次共速二者相对位移,由能量守恒得$\mu mgL_{2}=\dfrac{1}{2}m\left( \dfrac{v_{0}}{4} \right)^{2}+\dfrac{1}{2}m\left( \dfrac{v_{0}}{8} \right)^{2}-\dfrac{1}{2} \cdot 2m\left( \dfrac{v_{0}}{16} \right)^{2}$
解得$L_{2}=\dfrac{9v_{0}^{2}}{16\mu g} \cdot \dfrac{1}{16}$
以后每次情况均是如此,直至碰撞无数次后系统处于静止状态
此可得第$n$次碰撞后共速的速度$v_{n}=\dfrac{v_{0}}{4^{n}}$
第$n$次碰撞后至第$n$次共速二者相对位移$\mu mgL_{n}=\dfrac{1}{2}mv_{n-1}^{2}+\dfrac{1}{2}m\left( \dfrac{v_{n-1}}{2} \right)^{2}-\dfrac{1}{2} \cdot 2m\left( v_{n} \right)^{2}$
解得$L_{n}=\dfrac{9v_{0}^{2}}{16\mu g}\left( \dfrac{1}{16} \right)^{n-1}$
由等比数列求和公式可得$L=\sum\limits_{n=1}^{\infty}L_{n}=\dfrac{9v_{0}^{2}}{16\mu g}\left( \dfrac{1}{1-\dfrac{1}{16}} \right)=\dfrac{9v_{0}^{2}}{15\mu g}$
代入数据得$L=1.92\;\rm m$;
整个过程因摩擦产生的热量。
$Q=9.6\\;\\rm J$。
"]]摩擦生热$Q=\mu mgL=\dfrac{9mv_{0}^{2}}{15}$
代入数据得$Q=9.6\;\rm J$。
高中 | 动量守恒之木板滑块模型题目答案及解析(完整版)
