高中 | 带电粒子在叠加场中的运动问题 题目答案及解析
稿件来源:高途
高中 | 带电粒子在叠加场中的运动问题题目答案及解析如下,仅供参考!
选修3-1
第三章 磁场
3.6 带电粒子在匀强磁场中的运动
带电粒子在叠加场中的运动问题
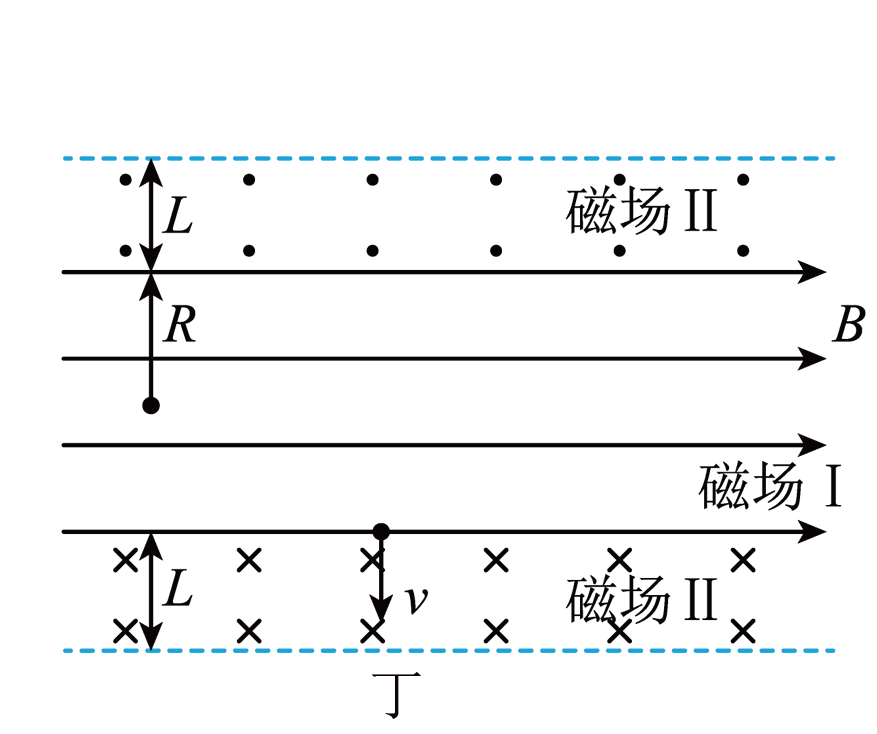
$2023$年$4$月,世界首个全超导托卡马克“东方超环”($\rm EAST$)成功实现了$403$秒稳态长脉冲高约束等离子体运行,创造了托卡马克装置高约束模式运行新的世界纪录。“人造太阳”研究的突破,代表着我国科技实力的系统性提升,中国站在了世界核聚变能源研究的前沿。某物理实验室对“人造太阳”磁约束模型进行模拟,立体图如图乙所示,半径为$R$的足够长水平圆柱形区域内分布水平向右的匀强磁场Ⅰ,磁感应强度大小为$B$;圆柱形磁场区域Ⅰ外侧分布有方向与磁场Ⅰ垂直的环形磁场Ⅱ,其磁感应强度大小处处相同也为$B$,其左视图与纵截面图分别如图丙、图丁所示。某时刻速度为$v=\dfrac{BqR}{m}$的氘原子核(已知氘原子核质量为$m$,电荷量为$q$)从水平磁场Ⅰ最低点竖直向下射入磁场Ⅱ,忽略粒子重力和空气阻力,不考虑相对论效应。求:

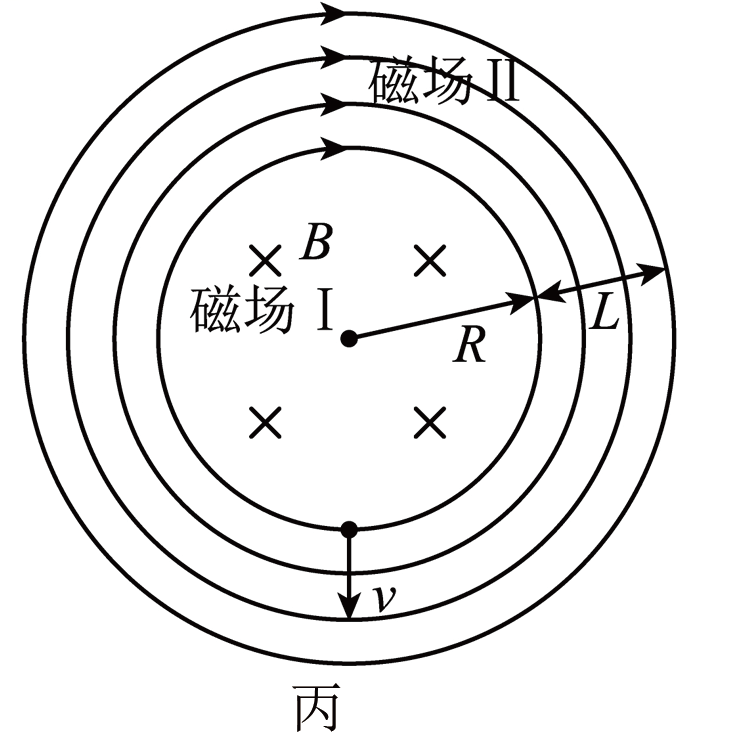
要想氘核不射出Ⅱ区磁场边界,Ⅱ区磁场的最小厚度$L$。
$L=R$
"]]洛伦兹力提供向心力$Bqv=\dfrac{mv^{2}}{L}$
将$v=\dfrac{BqR}{m}$代入,解得$L=R$
该氘原子核从出发后到第三次从Ⅱ区磁场返回Ⅰ区磁场边界的过程氘核运动的时间和位移大小,以及该过程中洛伦兹力的冲量;
$t=\\dfrac{4\\pi m}{Bq}$,$x=2\\sqrt{10}R$,$I=0$;
"]]氘在Ⅱ区域运动三个半圆,在Ⅰ区域运动$2$个$\dfrac{1}{4}$圆,(磁聚焦模型)根据圆周运动周期公式$Bqv=m\dfrac{4\pi^{2}}{T^{2}}R$
解得$T=\dfrac{2\pi m}{Bq}$
所以从出发后到第三次从Ⅱ区磁场返回Ⅰ区磁场边界的过程氘核运动的时间$t=3\times \dfrac{1}{2}\times \dfrac{2\pi m}{Bq}+2\times \dfrac{1}{4}\times\dfrac{2\pi m}{Bq}=\dfrac{4\pi m}{Bq}$
氘在Ⅱ区域的位移为$x_{2}=6R$
Ⅰ区域位移为$x_{1}=2R$
粒子从圆形磁场的最上方竖直向下返回,整个过程位移$x=\sqrt{{x_{1}}^{2}+{x_{2}}^{2}}=\sqrt{4R^{2}+36R^{2}}=2\sqrt{10}R$
洛伦兹力冲量$I=f_{洛}t=\Delta p=0$
在如图丁所示平面内磁场Ⅰ的下方,加上竖直向下的匀强电场 $E=2Bv$(图中未画出),若使氘核在此平面内从磁场Ⅰ的下边界以速度$v= \dfrac{BqR}{m}$水平射出,要保证氘核运动过程中不会从磁场Ⅱ的下边界射出,则磁场Ⅱ的厚度$L$需要满足什么范围,氘核在运动过程中的最小速度和最大速度分别是多少。
水平向左射出时,$L_{\\max}=6R$,向右$v_{\\max}=\\dfrac{5BqR}{m}$和向左$v_{\\min}= \\dfrac{BqR}{m}$,水平向右射出时,$L_{\\max}=2R$,向右$v_{\\max}=\\dfrac{3BqR}{m}$和向右$v_{\\min}=\\dfrac{BqR}{m}$
"]](配速法$1$)为了将电场力抵消掉,需要假定一个水平向右的速度$v_{1}$,此时满足洛伦兹力与电场力平衡$Bqv_{1}=Eq=2Bvq$
所以假定的速度为$v_{1}=2v$
若要满足水平向左的速度为$v$,还需要一个速度水平向左$v_{2}$,$v_{2}-v_{1}=v$,$v_{2}=3v$
所以原来复杂的运动可以看作是水平向右的$v_{1}$的匀速直线,与$v_{2}$的一个匀速圆周运动的叠加,根据圆周运动$\dfrac{m{(3v)}^{2}}{R_{{m}}}=Bq3v$,$R_{m}=3R$
所以磁场Ⅱ的厚度$L$为$L_{\max}=2R_{m}=6R$
向右最大速度与向左最小速度分别为$v_{\max}=v_{2}+v_{1}=5v=\dfrac{5BqR}{m}$,$v_{\min}=v_{2}-v_{1}=v=\dfrac{BqR}{m}$
(配速法$2$)为了将电场力抵消掉,需要假定一个水平向右的速度$v_{1}$,此时满足洛伦兹力与电场力平衡$Bqv_{1}=Eq=2Bvq$
所以假定的速度为$v_{1}=2v$
若要满足水平向右的速度为$v$,还需要一个速度水平向左$v_{3}$,$v_{1}-v_{3}=v$,$v_{3}=v$
所以原来复杂的运动可以看作是水平向右的$v_{1}$的匀速直线,与$v_{3}$的一个匀速圆周运动的叠加,根据圆周运动$\dfrac{mv^{2}}{R_{{m}}}=Bqv$,$R_{m}=R$
所以磁场Ⅱ的厚度$L$为$L_{\max}=2R_{m}=2R$
向右最大速度与向右最小速度分别为$v_{\max}=v_{2}+v_{1}=3v=\dfrac{3BqR}{m}$,$v_{\min}=v_{2}-v_{1}=v=\dfrac{BqR}{m}$
高中 | 带电粒子在叠加场中的运动问题题目答案及解析(完整版)
