| 动量守恒之木板滑块模型 题目答案及解析
稿件来源:高途
| 动量守恒之木板滑块模型题目答案及解析如下,仅供参考!
选修3-5
第十六章 动量守恒定律
16.3 动量守恒定律
动量守恒之木板滑块模型
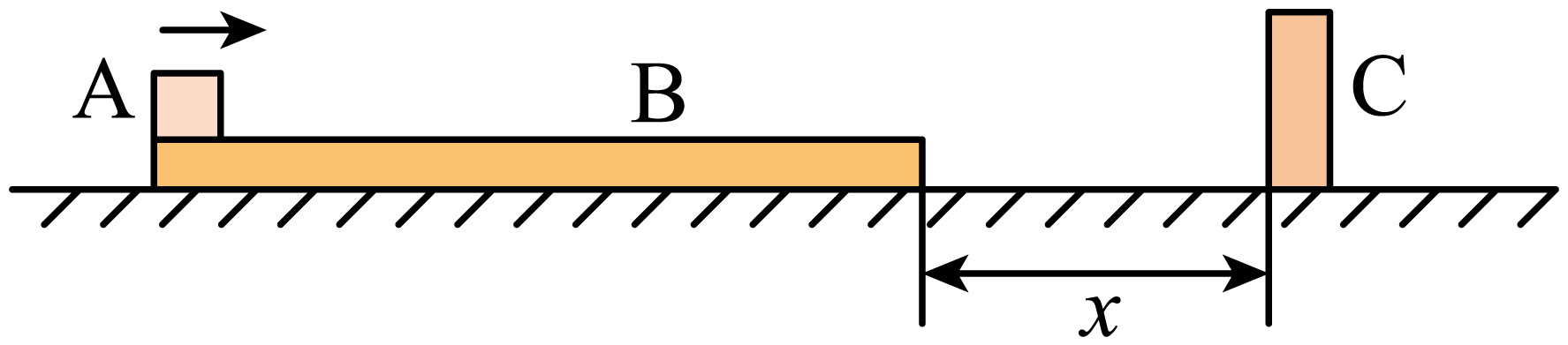
如图,质量为$2\;\rm kg$、足够长的长木板$B$静止在光滑水平地面上,在距长木板右端距离为$x$处有一固定挡板$C$,质量为$1\;\rm kg$的小滑块$A$从长木板的左端以大小为$12\;\rm m/s$的初速度滑上长木板,物块与长木板间的动摩擦因数为$0.4$,木板$B$与挡板$C$的碰撞过程中没有机械能损失且碰撞时间极短可忽略不计,取$g=10\;\rm m/s^{2}$。求:
若在$B$与$C$碰撞前$A$与$B$已相对静止,则$x$至少为多少;
$4\\;\\rm m$;
"]]$A$在$B$上做匀减速运动,$B$做匀加速运动,设$A$、$B$相对静止时,共同速度为$v_{1}$,根据动量守恒有$m_{A}v_{0}=(m_{A}+m_{B})v_{1}$
$B$运动加速度大小$a_{\text{B}}=\dfrac{\mu m_{\text{A}}g}{m_{\text{B}}}=2\;\rm \text{m}/\text{s}^{2}$
$B$运动的距离$x_{\text{B}}=\dfrac{v_{1}^{2}}{2a_{\text{B}}}=4\;\rm \text{m}$
因此,要使$B$与$C$碰撞前$A$与$B$已相对静止,则应$x\geqslant 4\;\rm m$。
若要使$B$与$C$第一次碰撞后,$B$向左运动的动量大小恰好等于$A$向右运动的动量大小,则最后$AB$静止,$B$不会再与$C$发生碰撞,求满足如上情况的$x$取值;
$x\\geqslant 1.125\\;\\rm m$;
"]]$B$与$C$碰撞后,当$A$向右的动量等于$B$向右动量时$m_{A}v_{A}=m_{B}v_{B}$
根据动量守恒有$m_{A}v_{0}=m_{A}v_{A}+m_{B}v_{B}$
$B$运动的距离${x'}_{\text{B}}=\dfrac{v_{\text{B}}^{2}}{2a_{\text{B}}}=2.25\;\rm \text{m}$
因此,应$x=2.25\;\rm m$。
若$x=0.25\;\rm m$,则$B$与$C$会碰撞几次。
$3$次
"]]当$x=0.25\;\rm m$时$x=\dfrac{1}{2}a_{\text{B}}t^{2}$
得$t_{1}=\dfrac{1}{2}\ \text{s}$
此时$v_{A1}=10\;\rm m/s$,$v_{B1}=1\;\rm m/s$
$B$与$C$碰撞后的速度大小为$v{^\prime}_{B1}=-1\;\rm m/s$
相邻两次碰撞的时间间隔$\Delta t=2\dfrac{v}{a_{\text{B}}}=1\;\rm \text{s}$
此时$v_{A2}=6\;\rm m/s$,$v_{B2}=1\;\rm m/s$
$B$与$C$再次碰撞后的速度大小为$v{^\prime}_{B2}=-1\;\rm m/s$
相邻两次碰撞的时间间隔$\Delta t=2\dfrac{v}{a_{\text{B}}}=1\;\rm \text{s}$
此时$v_{A3}=2\;\rm m/s$,$v_{B3}=1\;\rm m/s$
$B$与$C$第三次碰撞后的速度大小为$v{^\prime}_{B3}=-1\;\rm m/s$
此后不再碰撞,因此碰撞次数为$3$次。
| 动量守恒之木板滑块模型题目答案及解析(完整版)
