如图，竖直平面内有一光滑绝缘轨道，取竖直向上为$y$轴正方向，轨道形状满足曲线方程$y=x^{2}$。质量为$m$、电荷量为$q$（$q\gt 0$）的小圆环套在轨道上，空间有与$x$轴平行的匀强电场，电场强度大小$E=\dfrac{2mg}{q}$，圆环恰能静止在坐标（$1,1$）处，不计空气阻力，重力加速度$g$大小取$10$ $m/s^{2}$。若圆环由（$3,9$）处静止释放，则$(\qquad)$

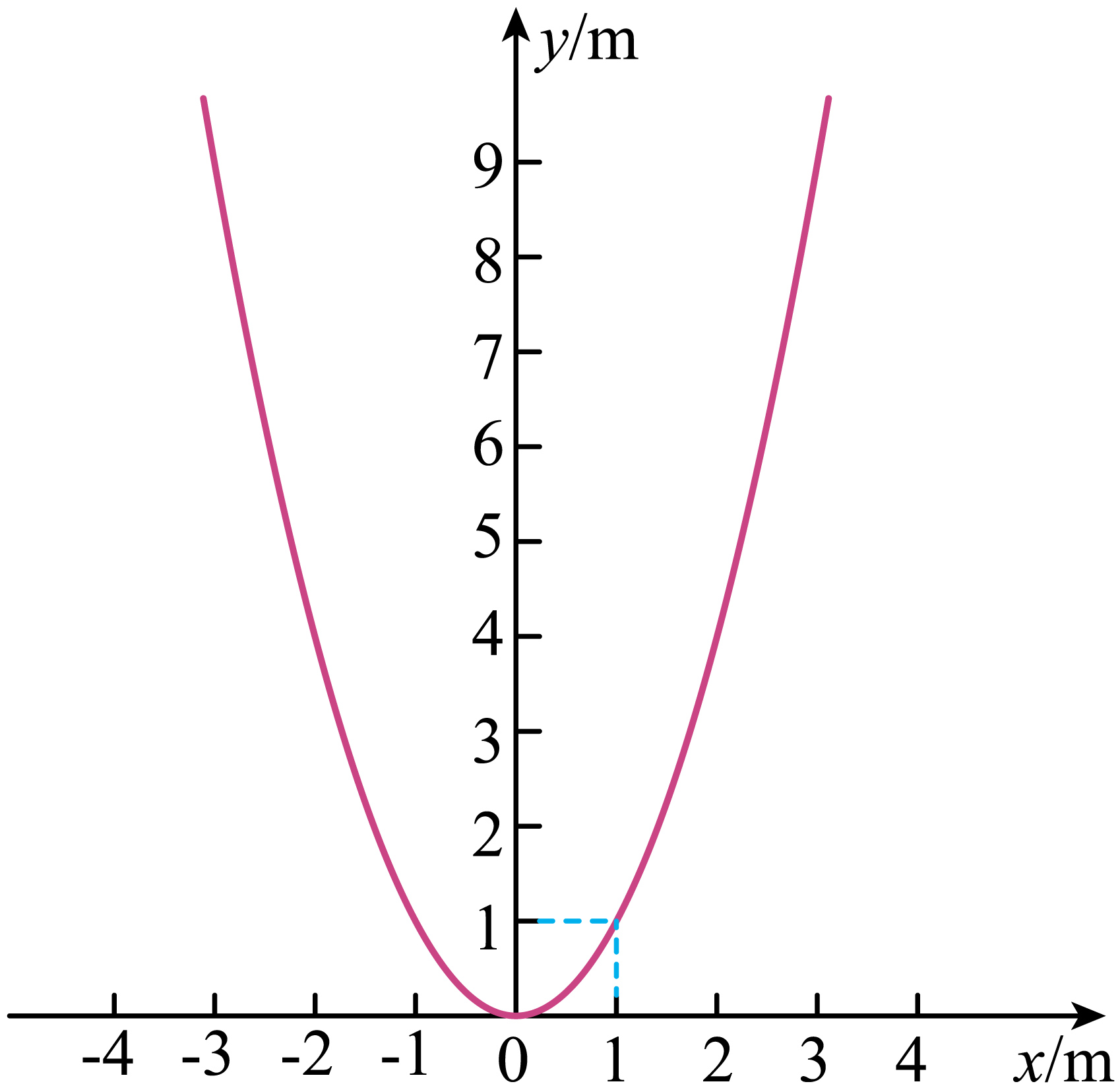
恰能运动到（$-3,9$）处

在（$1,1$）处加速度为零

在（$0,0$）处速率为$10\\sqrt{3}\\;\\rm \\text{m/s}$

在（$-1,1$）处机械能最小

$\rm AD$．由题意可知，圆环所受的电场力平行于$x$轴向右，如图所示

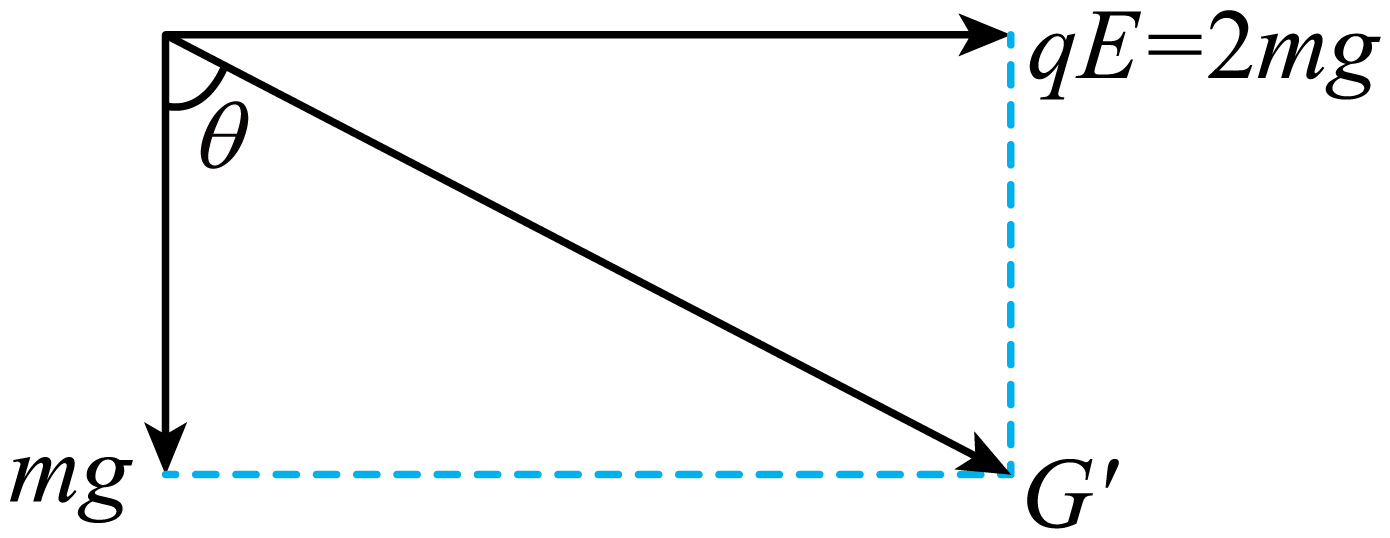
圆环所受重力与电场力的合力为$G'=\sqrt{(mg)^{2}+(qE)^{2}}=\sqrt{5}mg$

又$\tan\theta=\dfrac{qE}{mg}=2$

根据题意可知，坐标（$1,1$）处是等效最低点，过（$1,1$）做轨道的切线，再过坐标（$3,9$）作该切线的平行线，如图所示

根据题意写出该平行线的方程为$y-9=\tan \theta⋅(x-3)$

即$y=2x+3$

设该平行线与轨道的交点为$A$，则$A$点的坐标满足方程$y=2x+3$

$y=x^{2}$

解得$A$点的坐标为（$-1,1$），则圆环恰能运动到坐标（$-1,1$）。又圆环运动到该点时克服电场力做功最多，故机械能最小，故$\rm A$错误，$\rm D$正确；

$\rm B$．圆环做曲线运动，在（$1,1$）处加速度一定不为零，故$\rm B$错误；

$\rm C$．设圆环到达（$0,0$）处时的速度大小为$v$，则圆环由（$3,9$）处静止释放运动到（$0,0$）处的过程，由动能定理得$mgy-qEx=\dfrac{1}{2}mv^{2}$

又$E=\dfrac{2mg}{q}$

联立得$v=2\sqrt{15}\;\rm \text{m/s}$

故$\rm C$错误。

故选：$\rm D$。