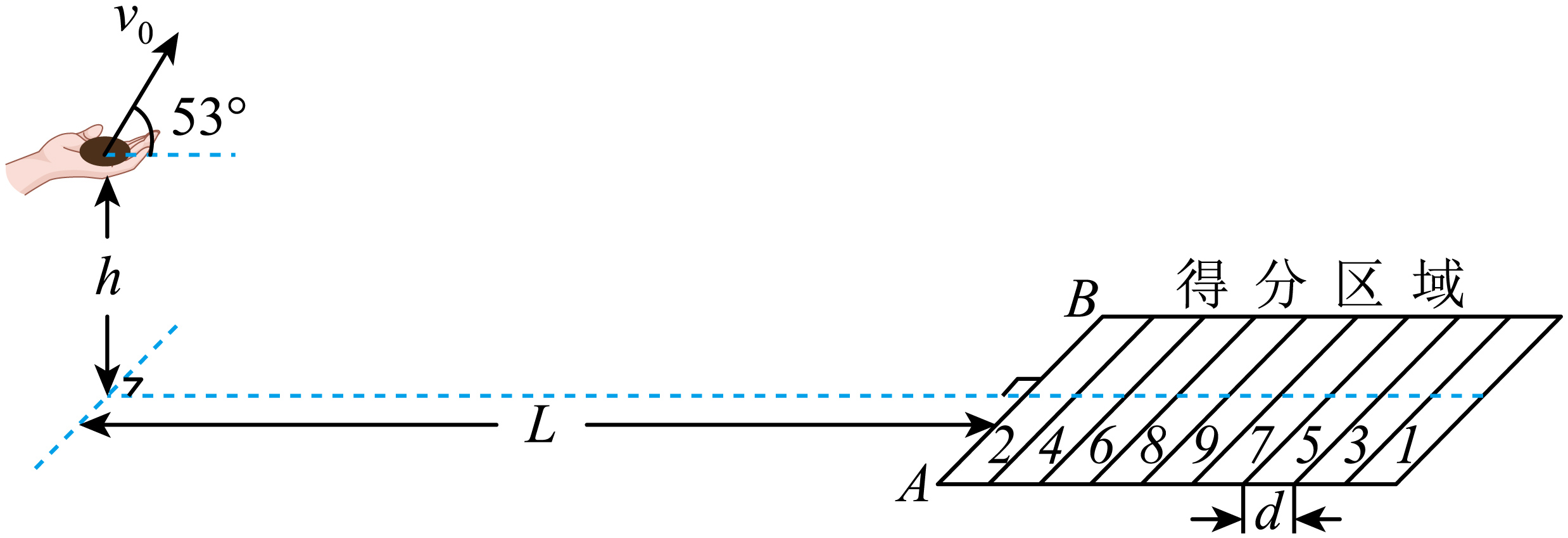
沙包从出手点到落地点的水平距离$x$；

$3\\ \\rm m$

沙包竖直上方的初速度为$v_{y}=v_{0}\sin 53^\circ =4\;\rm m/s$

沙包在竖直方向上减速到$0$，然后做自由落体运动，设竖直向上为正，则有$- h=v_{y}t-\dfrac{1}{2}gt^{2}$

代入数据解得$t=1\;\rm s$

沙包抛出的水平初速度为$v_{x}=v_{0}\cos 53^\circ =3\;\rm m/s$

所以从抛出到落地沙包的水平位移为$x=v_{x}t=3\;\rm m$

沙包与地面碰撞前、后动能的比值$k$。

$20$

沙包滑行的距离为$x_{0}=L+5d-x=0.45\;\rm m$

沙包滑行过程中，水平方向上有$f=\mu mg=ma$

的加速度大小$a=\mu g=2.5\;\rm m/s^{2}$

滑行的初速度有$v_{1}^{2}=2ax_{0}$

与地面碰撞后的动能$E_{\text{k2}}=\dfrac{1}{2}mv_{1}^{2}=\dfrac{9}{8}m$

从抛出到落地根据动能定理有$mgh=\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{0}^{2}$

解得落地瞬间的动能$E_{\text{k1}}=\dfrac{1}{2}mv^{2}=\dfrac{45}{2}m$

所以$k=\dfrac{E_{\text{k1}}}{E_{\text{k2}}}=20$