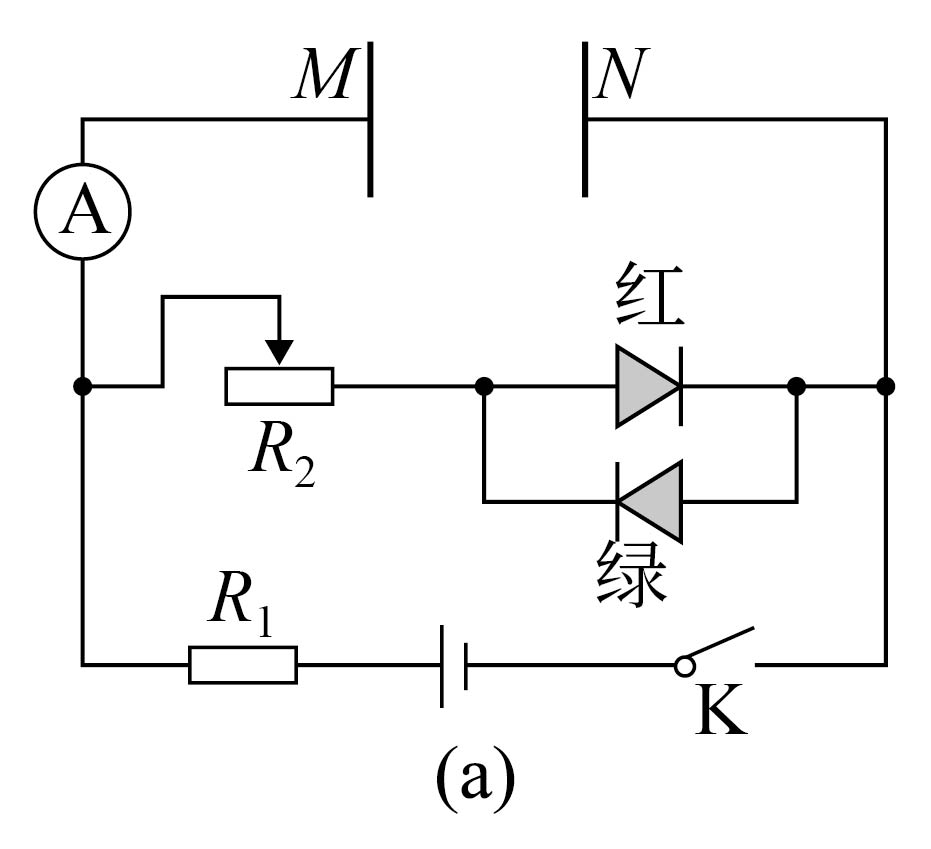
在二极管发光实验中：

①图（$a$）中，初始时电键$\rm K$闭合，在断开$\rm K$的瞬间，关于二极管发光的情况正确的是$(\qquad)$

$\;\rm A$．红色发光，绿色不发光                      $\;\rm B$．都发光

$\;\rm C$．绿色发光，红色不发光                      $\;\rm D$．都不发光

②电键$\rm K$断开，电容器放电；其他条件不变，若使$R_{2}$增大，则放电时间会$(\qquad)$

$\;\rm A$．不变              $\;\rm B$．增加              $\;\rm C$．减小

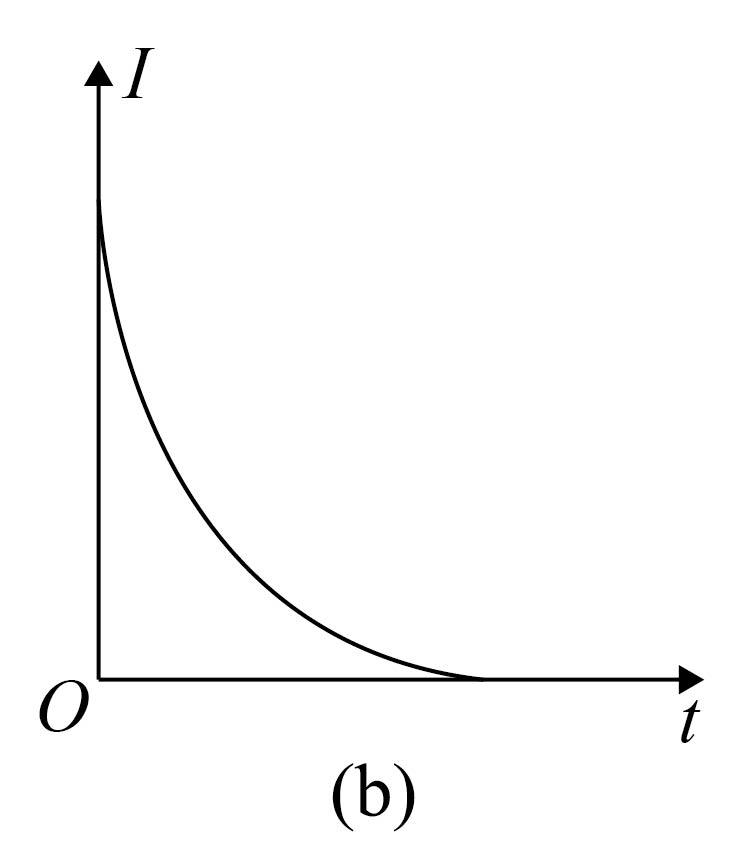
③如图（$b$）为电容器放电时，电流传感器测得的$I$–$t$图，请推测并画出：当$R_{2}$增大后，电容器放电时电流传感器测得的$I$–$t$图；

①$\\;\\rm A$②$\\;\\rm B$ ③图像见解析

①初始电键$\rm K$闭合时，电容器$M$端带正电，$N$端带负电；断开开关电容器放电，电流从$M$经发光二极管到$N$，由二极管的单向导通性可得红色发光，绿色不发光；故$\;\rm A$正确；

②电键$\rm K$断开，电容器放电；其他条件不变，若使$R_{2}$增大，则放电的平均电流变小，而放电的电荷量不变，由$Q=\overline{I}t$可得放电时间会增加；故$\;\rm B$正确；

③$R_{2}$增大后，放电的最大电流变小；但总的电荷量不变，由$I$–$t$图围成的面积表示电荷量，故面积不变时间变长。故图如下：

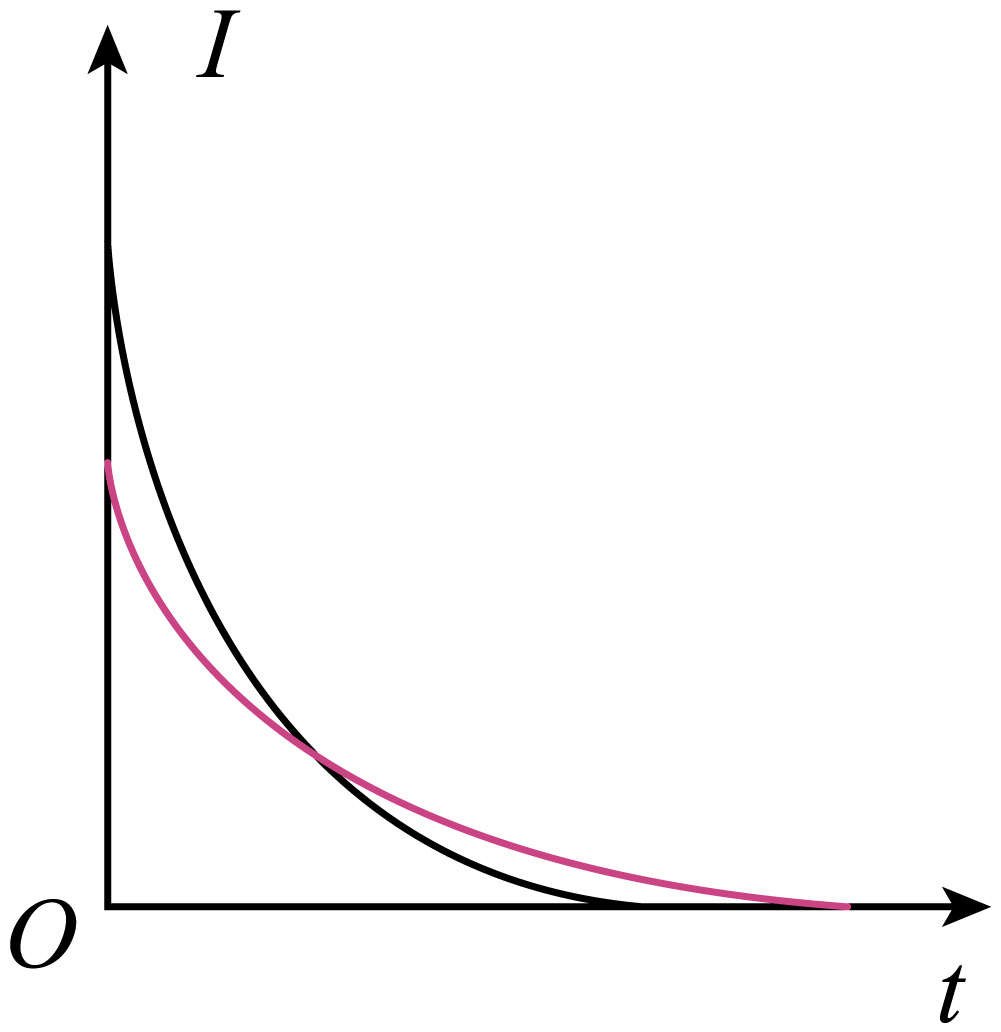
图（$a$）中，电源电动势为$E=10\;\rm V$，忽略电源内阻和二极管电阻，$R_{1}=5\;\rm \Omega$，$R_{2}$最大阻值为$10\;\rm \Omega$。则$R_{2}$功率的最大值为                 $\;\rm W$；此时电容器的电压$U_{MN}=$                 $\;\rm V$；

把$R_{1}$等效为电源的内阻，则$R_{2}$消耗功率即为电源的输出功率；由规律可知当外电阻等于内阻的时候，电源的输出功率最大即$R_{2}$的功率最大，最大功率$P_{\text{m}}=\dfrac{E^{2}}{4r}= \dfrac{E^{2}}{4R_{1}}$

代入数据得$P_{\rm m}=5\;\rm W$；

此时电容器两端的电压就等于$R_{2}$两端的电压，即$U_{{MN}}=U_{{R2}}=\dfrac{R_{2}}{R_{1}+R_{2}}E=5\;\rm {V}$；

在图（$a$）中，保持电键$K$闭合，完成充电的电容器$MN$竖直放置，如图（$c$），其长为$L$，宽为$d$，金属板间电压为$U_{MN}$，在两板中间区域加垂直于纸面的匀强磁场。质量为$m$、电量为$q$的带电油滴从板上高$h$处由静止自由下落，并经两板上端中央$P$点进入板间，油滴在$P$点所受的电场力与洛伦兹力恰好大小相等方向相反，且最后恰好从金属板的下边缘离开。空气阻力不计，重力加速度为$g$。

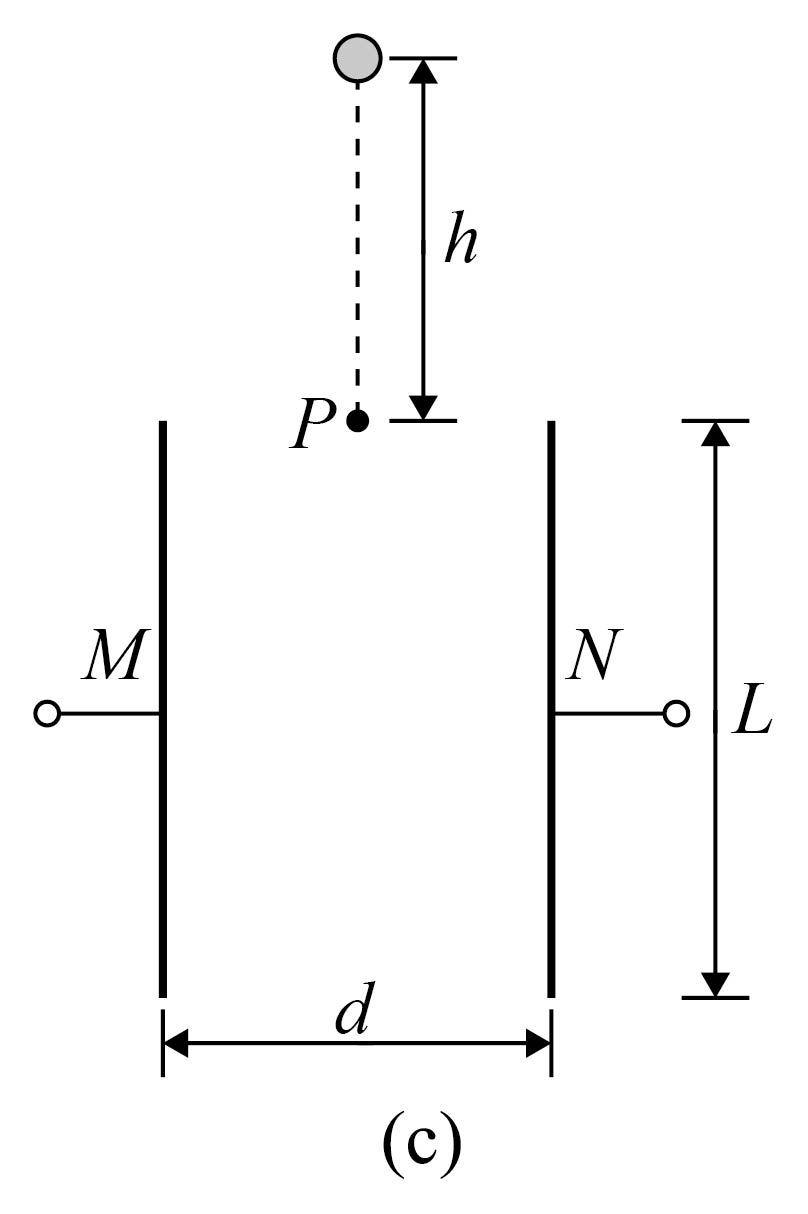
①下列说法正确的是                 。

$\;\rm A$．磁场方向垂直于纸面向里      $\;\rm B$．磁场方向垂直于纸面向外

$\;\rm C$．可以判断油滴带正电          $\;\rm D$．油滴的电性不能确定

②$P$点的电场强度$E=$                 。

③油滴离开金属板时的动能$E_{\rm k}=$                 。

①已知电场的方向由$M$指向$N$，假设油滴带正电，则所受电场力向右；油滴在$P$点所受的电场力与洛伦兹力恰好大小相等方向相反，由左手定则可判定磁场方向垂直于纸面向外。再假设油滴带负电，则所受电场力向左，洛伦兹力的方向向右；再由左手定则可得磁场方向还是垂直于纸面向外；故$\;\rm BD$正确。

②由匀强电场中电场强度的定义可得$E=\dfrac{U}{d}=\dfrac{U_{{MN}}}{d}$。

③由油滴在$P$点所受的电场力与洛伦兹力恰好大小相等方向相反，接下来油滴速度增大，洛伦兹力会大于电场力，故最后恰好从金属板的下边缘离开时，电场力一直做负功；由全过程运用动能定理得$mg(h+L)-\dfrac{1}{2}qU_{{MN}}=E_{\text{k}}-0$

即$E_{{\rm k}}=mg(h+L)-\dfrac{1}{2}qU_{{MN}}$。