| 波的多解问题 题目答案及解析
稿件来源:高途
| 波的多解问题题目答案及解析如下,仅供参考!
选修3-4
第十二章 机械波
12.2 波的图像
波的多解问题
在$2024$年巴黎奥运会的艺术体操个人全能决赛中,中国选手王子露巧妙地将中国风融入舞蹈编排,最终获得总分第七,创造了我国历史最佳战绩。在带操比赛过程中,她挥舞彩带形成的波有时类似于水平方向传播的简谐横波,如图($a$)所示,且波速约为$v=3.0\;\rm m/s$。

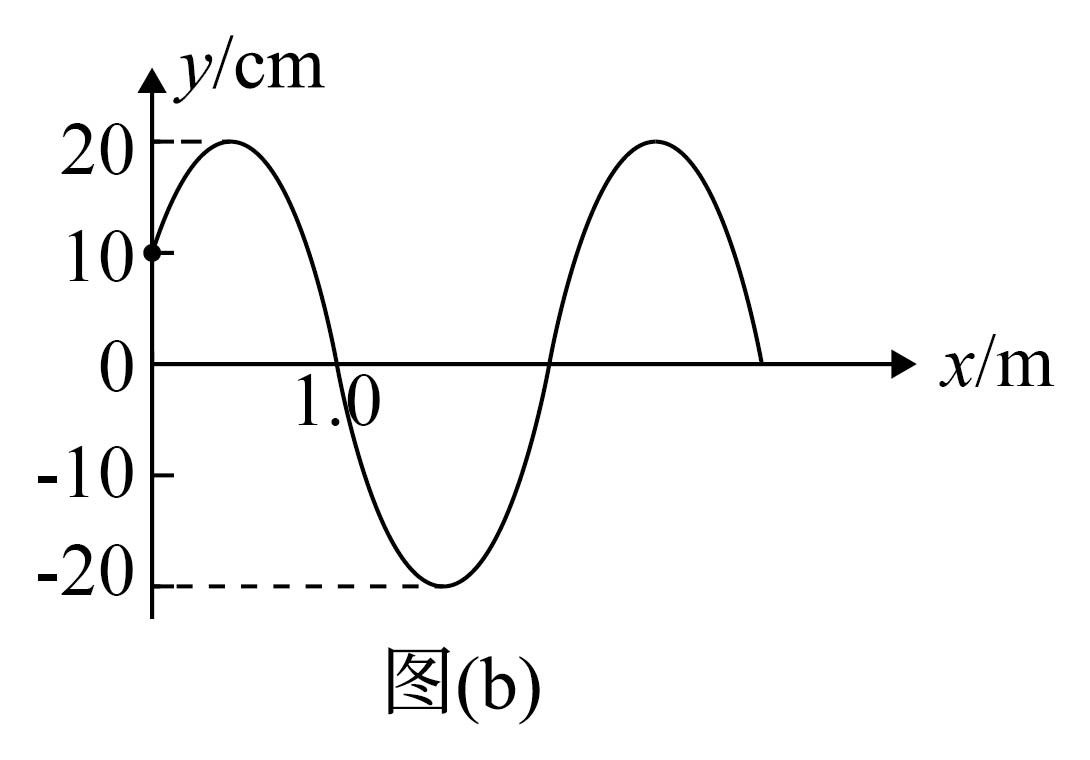
在某$t=0$时刻,彩带上的一段波形可简化为如图($b$)所示的简谐横波,此时彩带上质点$P$的位移$y=10\;\rm cm$,且沿$y$轴负方向振动。则该简谐横波的波长$\lambda=$ $\;\rm m$;彩带上位置坐标$x=1.0\;\rm m$的质点偏离平衡位置的位移$y$与时间$t$的关系式可表示为$y=$ ,用$T$表示这列波的周期,则从图示时刻起,该质点的加速度$a$随时间$t$变化的图像可能为 ;
$A$.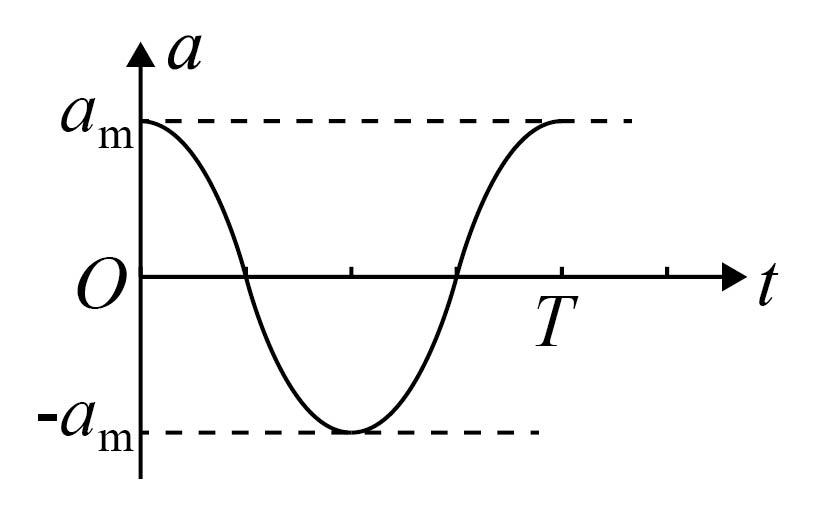 $B$.
$B$.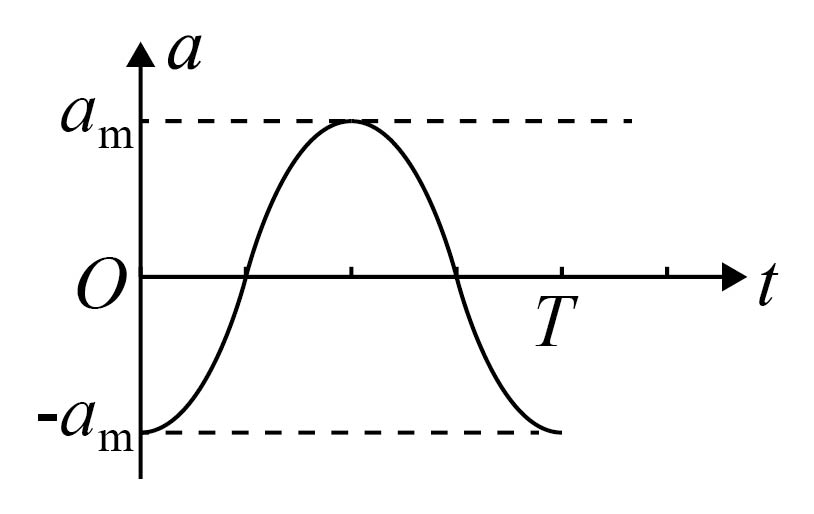
$C$. 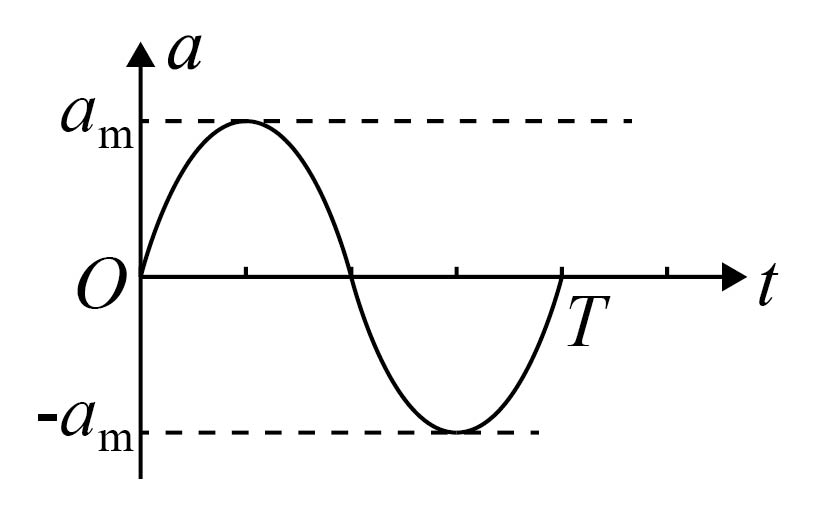 $D$.
$D$.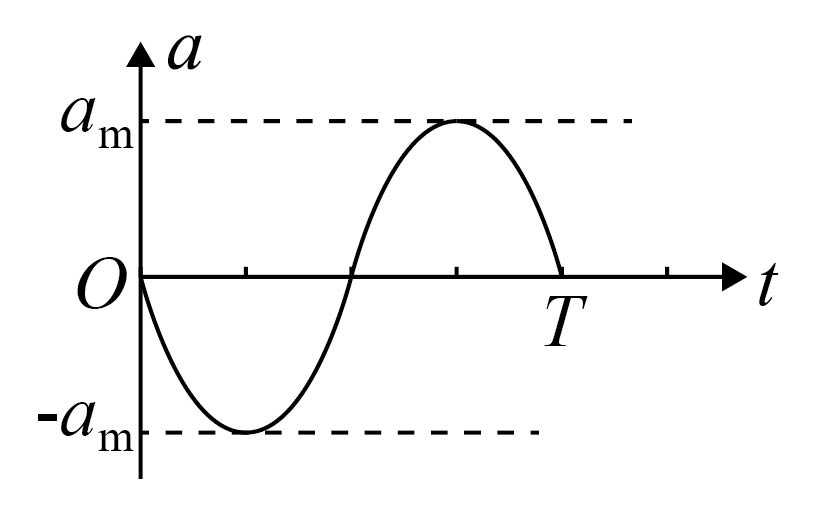
由图可知$\dfrac{\lambda}{6} +\dfrac{\lambda}{4}=1.0\;\rm \text{m}$
可得波长$\lambda=2.4\;\rm m$
因$A=0.2\;\rm m$周期$T=\dfrac{\lambda}{v}=0.8\;\rm \text{s}$
则彩带上位置坐标$x=1.0\;\rm m$的质点在$t=0$时刻向下振动,则偏离平衡位置的位移$y$与时间$t$的关系式可表示为$y=0.2\sin\left(\dfrac{\text{5}}{\text{2}}\pi t\right){\;\rm m}$
因在$t=0$时刻该质点在平衡位置向下振动,可知加速度$a$随时间变化图像为$\rm D$所示;
王子露在另一段时间内甩出的彩带波可简化为如图($c$)所示的简谐横波,其中实线为$t_{1}$时刻的波形图,虚线为$t_{2}$时刻的波形图,已知$\Delta t=t_{2}−t_{1}=0.75\;\rm s$,关于该简谐横波,下列说法正确的是$(\qquad)$
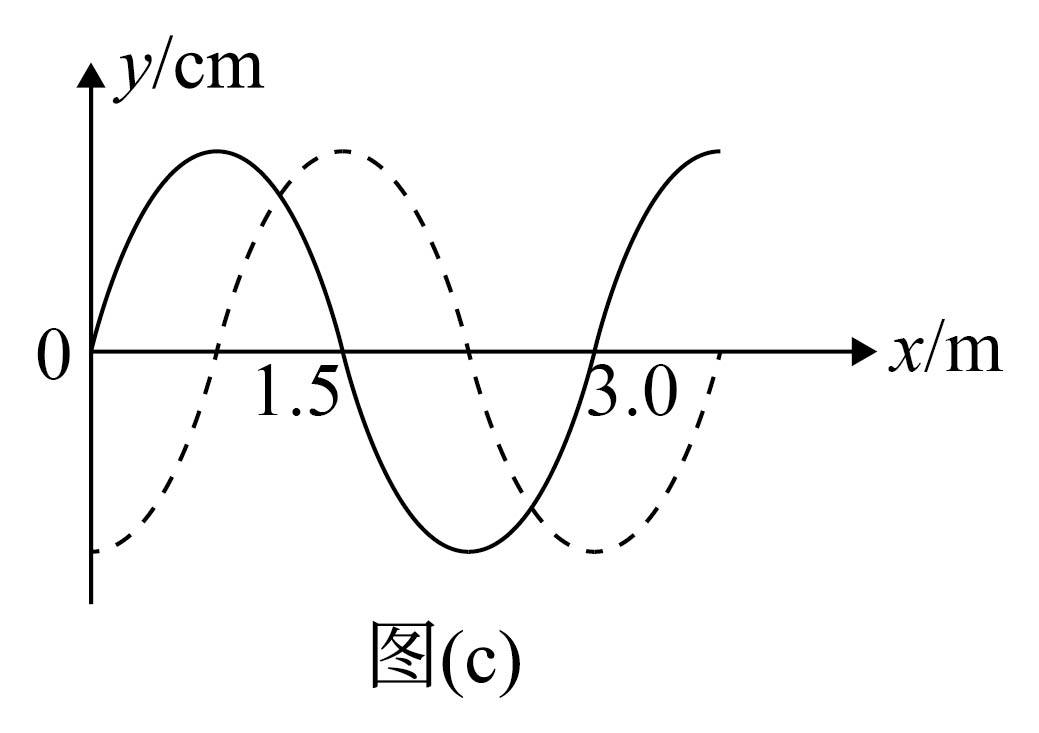
可能沿$x$轴正方向传播
","$t_{1}$时刻,$x=1.5\\;\\rm m$处的质点速度大小等于$3\\;\\rm m/s$
","若王子露的手振动加快,形成的简谐横波波速不变
","从$t_{1}$时刻开始,为使$x=0.75\\;\\rm m$处的质点位于波谷,需再经历时间$t=0.5n\\rm s$,$n=1$,$2$,$3$……
"]$\rm A$.该波波长为$3\;\rm m$则周期为$T'= \dfrac{\lambda'}{v}=1\;\rm \text{s}$
在$\Delta t=0.75{\;\rm s}=\dfrac{3}{4}T'$
可知波向$0.75\;\rm s$内波沿$x$轴负方向传播,选项$\rm A$错误;
$\rm B$.$t_{1}$时刻,$x=1.5\;\rm m$处的质点振动速度最大,但不一样等于$3\;\rm m/s$,选项$\rm B$错误;
$\rm C$.波速由介质决定,与振源振动频率无关,选项$\rm C$正确;
$\rm D$.从$t_{1}$时刻开始,为使$x=0.75\;\rm m$处的质点位于波谷,需再经历时间
$t=nT'+\dfrac{T'}{2}=(n+0.5){\;\rm s}$, $n=1$,$2$,$3$……,选项$\rm D$错误。
故选:$\rm C$;
为了记录王子露在比赛中的精彩瞬间,有人抓拍了很多照片,其中一张照片,由于拍摄视角的问题,有一部分彩带被前排观众挡住了。经过观察,发现该彩带形状可简化为如图($d$)所示的沿$x$轴正方向传播的简谐横波,其中虚线框区域内彩带波缺失,在图($d$)中补全彩带被挡住的波形;
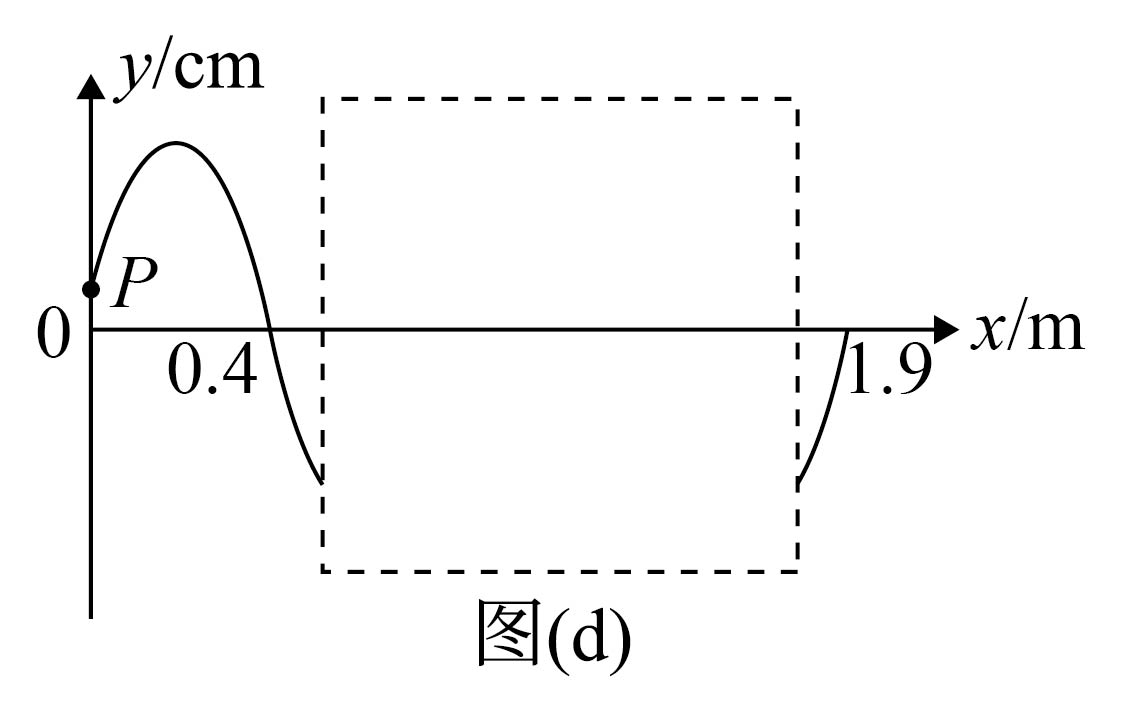
见解析
"]]由图($d$)可知:$\dfrac{1}{4}\lambda\lt 0.4\;\rm m$,$\dfrac{1}{2}\lambda\gt 0.4\;\rm m$,即$0.8\;\rm m\lt \lambda\lt 1.6\;\rm m$
又根据$0.4\;\rm m \sim 1.9\;\rm m$之间的波形图可知$(1.9-0.4){\;\rm m}=\left(n+\dfrac{{1}}{{2}}\right)\lambda$,其中$n=0$,$1$,$2$,……
即$\left(n+\dfrac{\text{1}}{\text{2}}\right)\times 0.8\lt \left(n+\dfrac{\text{1}}{\text{2}}\right)\lambda\lt \left(n+\dfrac{\text{1}}{\text{2}}\right)\times 1.6$
或 $\left(n+\dfrac{\text{1}}{\text{2}}\right)\times 0.8\lt 1.5\lt \left(n+\dfrac{\text{1}}{\text{2}}\right)\times 1.6$
解得$\dfrac{\text{7}}{\text{16}}\lt n\lt \dfrac{\text{11}}{\text{8}}$
即$n=1$
则 $\lambda=\dfrac{1.5}{1+\dfrac{1}{2}}\;\rm m=1.0\;\rm m$
即$x$轴上$0.4\;\rm m\sim 1.9\;\rm m$之间有$1\dfrac{1}{2}$个波长,可由此将($1$)中波形如图($f$)所示补全:
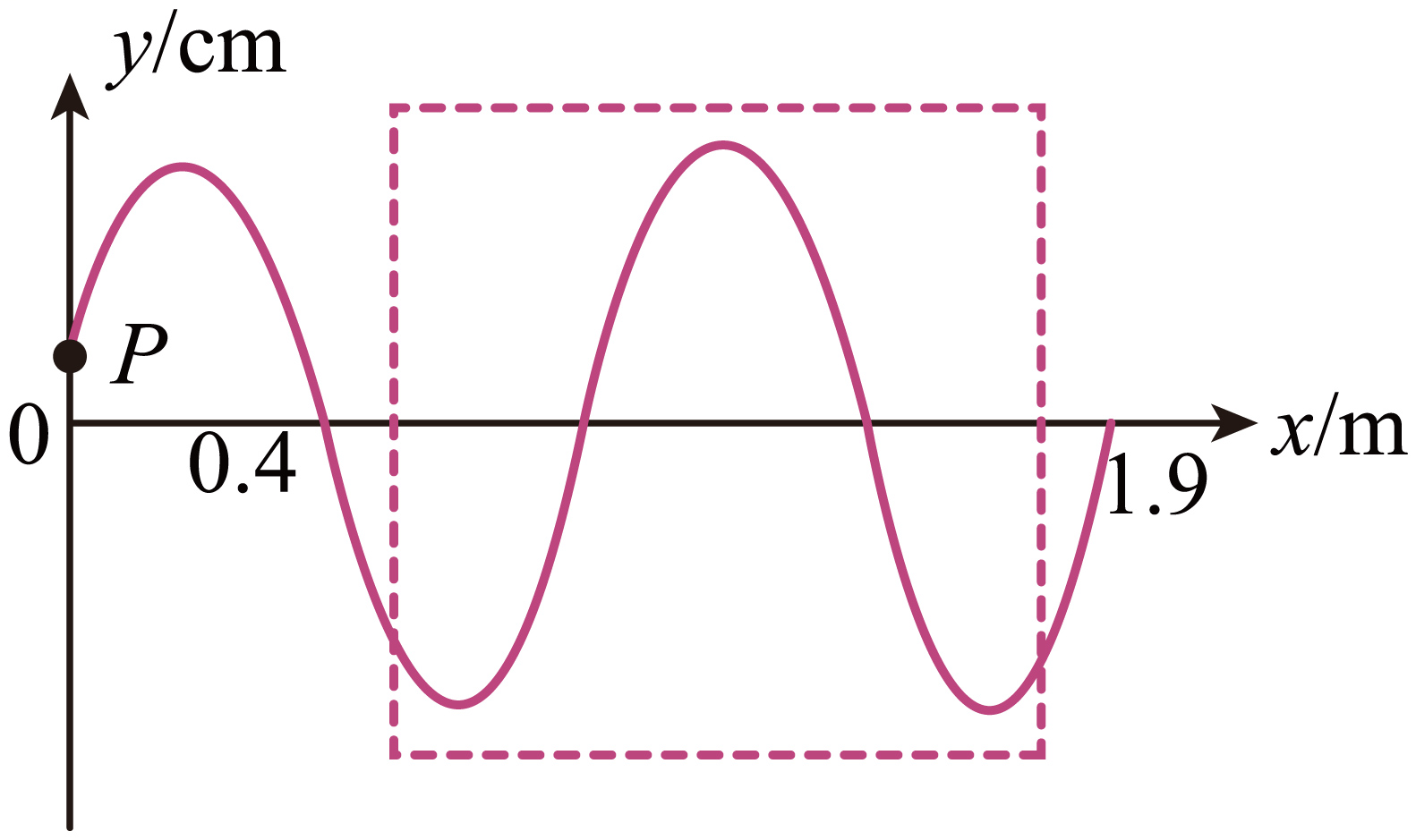
从图示时刻开始,再经过$t=0.2\;\rm s$,彩带上的$P$质点将位于 (选填:“波峰”、“波谷”或“平衡位置”),请通过计算说明判断的依据 。(论证)
平衡位置 ;见解析
"]]根据常识,比赛中使用的是同一根彩带,所以彩带波的波速仍为$v=3.0\;\rm m/s$
法一:则从图示时刻起,再经过$t=0.2\;\rm s$,波向$x$轴正方向传播的距离为$x=vt=3.0\times 0.2\;\rm m=0.6\;\rm m$
由于这列彩带波的波长为$1.0\;\rm m$,半波长为$0.5\;\rm m$
则彩带波上的质点$P$到其左侧第一个平衡位置的距离$x_{1}=(0.5-0.4)\;\rm m=0.1\;\rm m$
而$0.6\;\rm m=0.1\;\rm m+0.5\;\rm m=0.1\;\rm m+\dfrac{\text{1}}{\text{2}}\lambda$
即再经过$t=0.2\;\rm s$,相当于$P$左侧第二个处于平衡位置的质点振动状态传递到$P$点。
法二:这列波的周期为$T=\dfrac{\lambda}{v}=\dfrac{1}{3}\;\rm s$
以图示时刻为零时刻,设质点$P$的振幅为$A$,则其振动方程可写为
$y=A\sin\left(\dfrac{2\pi}{{T}}t+\dfrac{4\pi}{\text{5}}\right)=A\sin\left(\dfrac{2\pi}{\dfrac{\text{1}}{\text{3}}}t+\dfrac{4\pi}{\text{5}}\right)=A\sin\left(6\pi t+\dfrac{4\pi}{\text{5}}\right)$
将$t=0.2\;\rm s$代入,可得此时质点$P$的位移$y=A\sin\left(6\pi \times 0.2+\dfrac{4\pi}{\text{5}}\right)=A\sin(2\pi)=0$
即此时质点$P$位于平衡位置。
| 波的多解问题题目答案及解析(完整版)
