高中 | 带电粒子在组合场中的运动问题 题目答案及解析
稿件来源:高途
高中 | 带电粒子在组合场中的运动问题题目答案及解析如下,仅供参考!
选修3-1
第三章 磁场
3.6 带电粒子在匀强磁场中的运动
带电粒子在组合场中的运动问题
如图所示,半径$r=0.06\;\rm m$的半圆形无场区的圆心在坐标原点$O$处,半径$R=0.1\;\rm m$,磁感应强度大小$B=0.075\;\rm T$的圆形有界磁场区的圆心坐标为$(0, 0.08\;\rm m)$,平行金属板$MN$的极板长$L=0.3\;\rm m$,$M$板位于$y=0.18\;\rm m$处,$N$板位于$x$轴。其中$\rm N$极板收集到的粒子全部中和吸收。一位于$O$处的粒子源向第一、二象限均匀地发射速度为$v$的带正电粒子,经圆形磁场偏转后,从第一象限出射的粒子速度方向均沿$x$轴正方向,已知粒子在磁场中的运动半径$R_{0}=0.08\;\rm m$,若粒子重力不计、比荷$\dfrac{q}{m}=10^{8}\;\rm \text{C}/\text{kg}$、不计粒子间的相互作用力及电场的边缘效应。
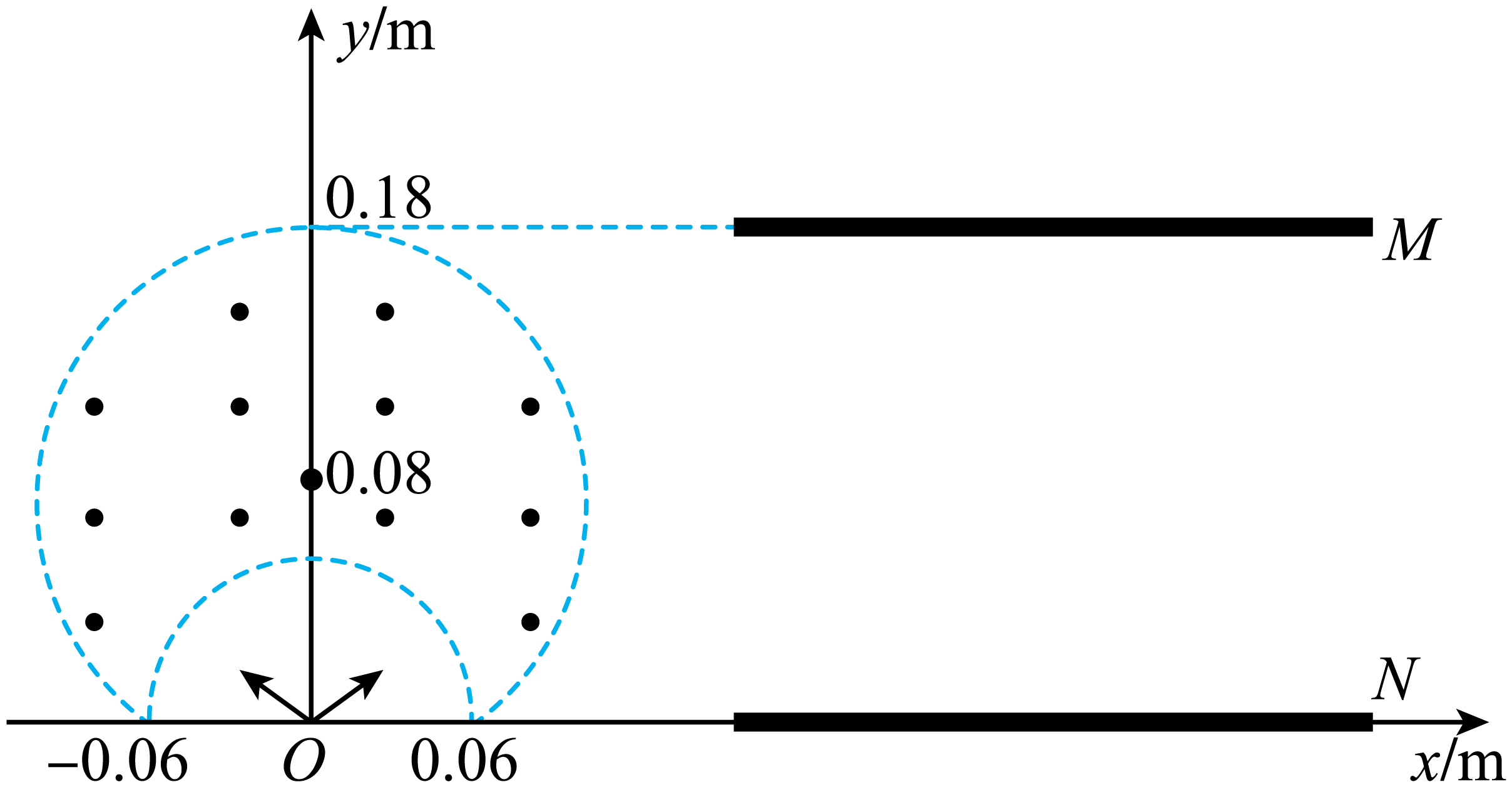
求粒子的发射速度$v$的大小;
$v=6.0 \\times 10^{5}\\;\\rm m/s$
"]]根据洛伦兹力提供向心力有$qvB=m\dfrac{v^{2}}{R_{0}}$
解得$v=6.0 \times 10^{5}\;\rm m/s$;
若粒子从$O$点沿$y$轴正方向射入磁场,求它离开磁场时的坐标;
$(0.08\\;\\rm m,0.14\\;\\rm m)$
"]]粒子从$O$点沿$y$轴正方向射入磁场,如图
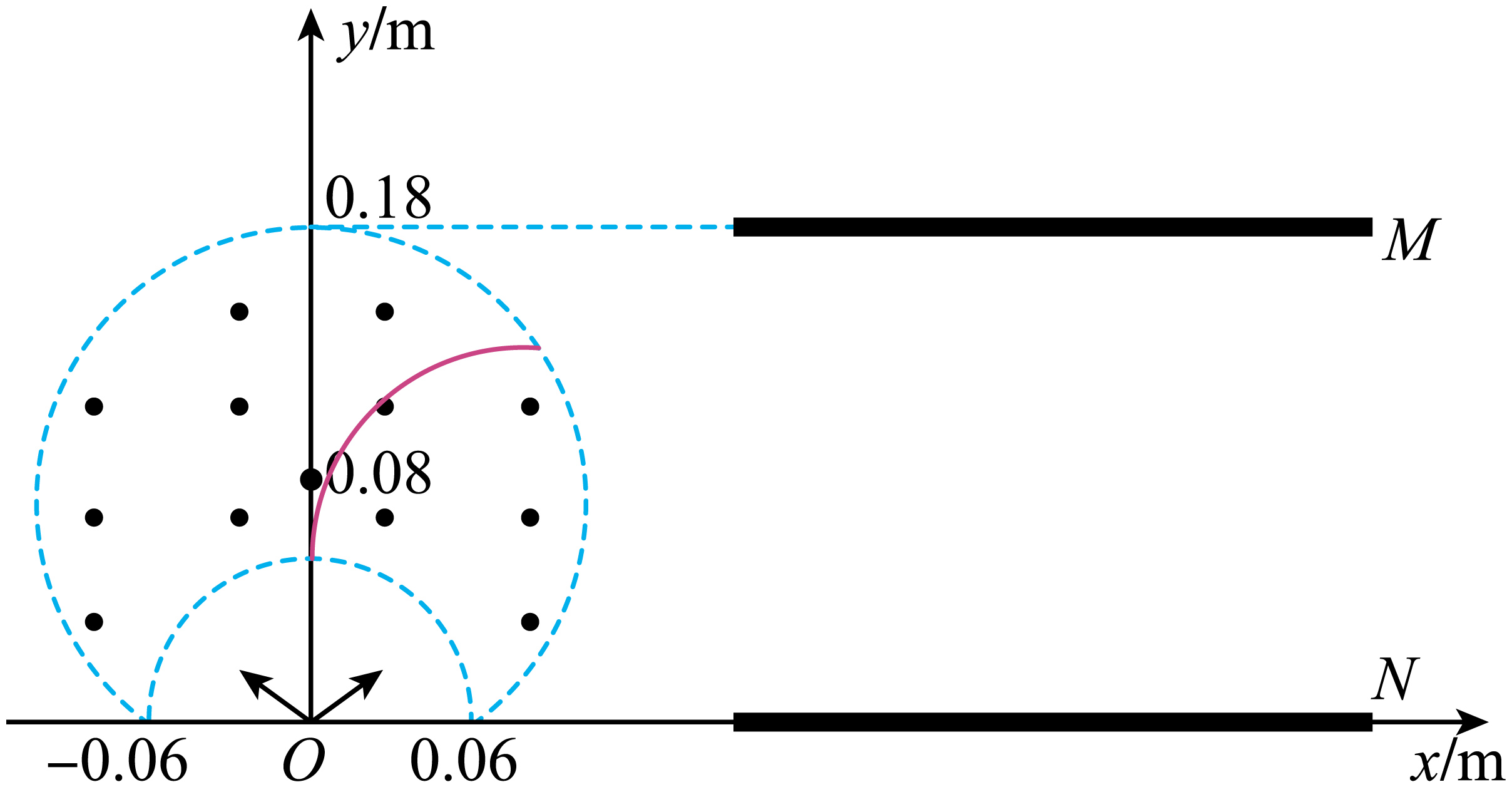
根据几何关系可知离开磁场时有
$y=0.06\;\rm m+0.08\;\rm m=0.14\;\rm m$
$x=0.08\;\rm m$
离开磁场时的坐标为$(0.08\;\rm m,0.14\;\rm m)$;
要使进入极板间的粒子都被$N$板收集,则$M$、$N$板间所加的电压至少多大?上述临界情况时粒子在电场中的加速度多大?
$a=1.44 \\times 10^{13}\\;\\rm m/s^{2}$,$U=2592\\;\\rm V$
"]]从坐标$(0,0.18\;\rm m)$处射出磁场的粒子,打到$N$点时对应的$M$、$N$板间所加的电压最小,则有$L=vt$,$y=\dfrac{1}{2}at^{2}$
根据牛顿第二定律有$a=\dfrac{qU}{my}$
解得$a=1.44 \times 10^{13}\;\rm m/s^{2}$,$U=2592\;\rm V$。
高中 | 带电粒子在组合场中的运动问题题目答案及解析(完整版)
