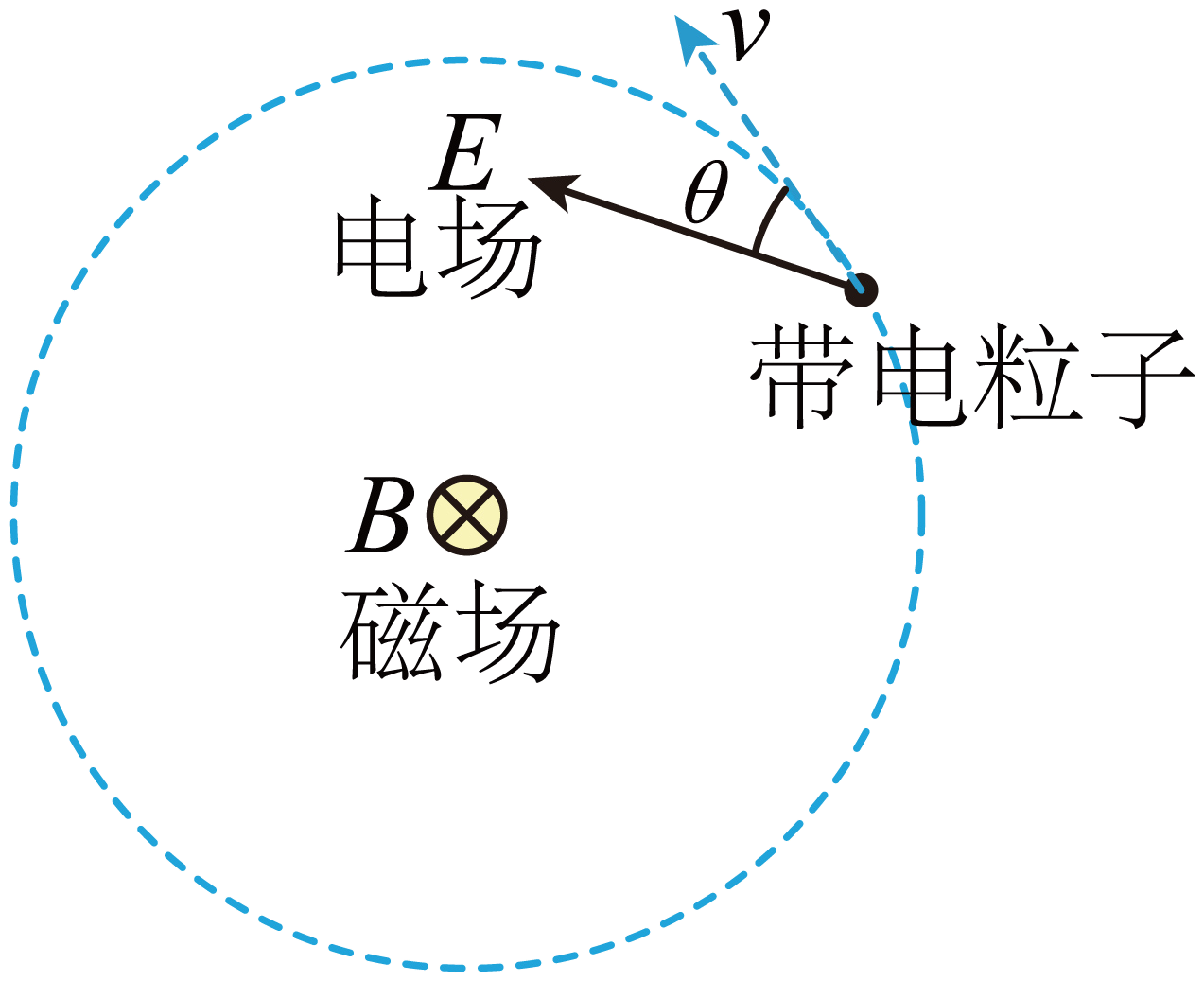
求$E=0$，$k=$ $0$时，带电粒子运动的角速度$\omega_{0}$；

$\\omega_{0}= \\dfrac{qB}{m}$；

题意知$E=0$，$k=$ $0$时，带电粒子只受洛伦兹力作用，则有$qvB=m\dfrac{v^{2}}{r}$

因为$v=\dfrac{2\pi r}{T}$

联立整理得带电粒子运动的周期$T=\dfrac{2\pi m}{qB}$

带电粒子运动的角速度$\omega_{0}=\dfrac{2\pi}{T}=\dfrac{qB}{m}$；

求带电粒子运动速度的大小$v$和$\tan\theta$（用$m$、$\omega$、$k$、$q$、$B$和$E$表示）；

$v= \\dfrac{qE\\cos\\theta}{k}$，$\\tan\\theta= \\dfrac{m\\omega-qB}{k}$；

带电粒子在水平面内做匀速率圆周运动，则粒子在运动方向上所受合力为零，则有$qE\cos \theta=kv$

解得带电粒子运动速度的大小$v=\dfrac{qE\cos\theta}{k}$

洛伦兹力与电场力的分力的合力提供向心力$qvB+qE\sin\theta=m\dfrac{v^{2}}{r}$

又$\omega=\dfrac{v}{r}$

联立解得$\tan\theta=\dfrac{m\omega-qB}{k}$；

求电场力的功率及功率的最大值；

$\\dfrac{q^{2}E^{2}\\cos^{2}\\theta}{k}$，$\\dfrac{q^{2}E^{2}}{k}$；

因为功率$P=Fv\cos \theta$

故电场力的功率$P_{电}=qEv\cos\theta=\dfrac{q^{2}E^{2}\cos^{2}\theta}{k}$

当$\theta=0^\circ$时，功率的最大值$P_{\rm m}=\dfrac{q^{2}E^{2}}{k}$；

若电场力的功率减小为最大值的一半，求速度。

$\\dfrac{qE}{2k\\cos\\theta}$。

若电场力的功率减小为最大值的一半，则$P_{电1}=\dfrac{1}{2}P_{\rm{m}}=\dfrac{q^{2}E^{2}}{2k}=Eqv\cos\theta$

解得$v=\dfrac{qE}{2k\cos\theta}$。