高中 | 斜面问题 题目答案及解析
稿件来源:高途
高中 | 斜面问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
斜面问题
如图所示,光滑斜面$AB$与水平方向成$\theta=30^\circ$的传送带$BC$平滑连接,传送带以速率$v= \dfrac{1}{2}\sqrt{gL}$顺时针转动,$AB$与$BC$的长度均为$L$,质量为$m$的小物块在水平推力作用下静止在$A$点,小物块与传送带间的动摩擦因数$\mu= \dfrac{\sqrt{3}}{3}$,重力加速度为$g$。
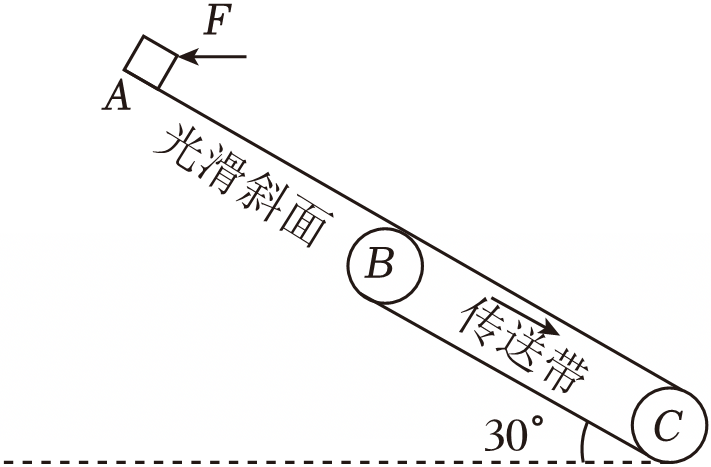
求水平推力的大小$F$;
[["
$\\dfrac{\\sqrt{3}mg}{3}$
"]]根据共点力平衡条件可知$\tan30^\circ= \dfrac{F}{mg}$
解得$F= \dfrac{\sqrt{3}mg}{3}$
若撤去推力,求:
①物块到达传送带$B$点时的加速度大小$a$;
②物块从$A$运动$C$的时间$t$。
[["
$0$;$3\\sqrt{\\dfrac{L}{g}}$
"]]①撤去推力,物块到达传送带$B$点时,速度满足$v^{2}=2g\sin30^\circ L$
解得$v= \sqrt{gL}$
根据牛顿第二定律有$mg\sin30^\circ-\mu mg\cos30^\circ=ma$
解得$a=0$
②在光滑斜面运动的时间为$L= \dfrac{1}{2}vt_{1}$
在传送带匀速运动,时间为$t_{2}= \dfrac{L}{v}$
物块从$A$运动$C$的时间$t=t_{1}+t_{2}$
解得$t=3\sqrt{\dfrac{L}{g}}$
高中 | 斜面问题题目答案及解析(完整版)
去刷题
相关题库:
滑沙运动是继滑冰、滑水、滑雪,还有滑草之后另一新兴运动,它使户外运动爱好者在运动的同时又能领略到沙漠的绮丽风光。此项目尤其博得青年人的喜爱。某景区由于滑道较长、较陡峭,人滑到底端时速度过大,极具危险性。为此,某同学提出了如下设想,在滑道底端设置一个较长的传送带,利用传送带对人和滑沙板进行减速,简化模型如图所示。倾斜传送带沿顺时针方向以的速度匀速转动,传送带的长,倾角,传送带左侧是倾斜滑道,滑道底端通过一小段光滑圆弧轨道与传送带下端衔接,圆弧轨道两端分别与斜面和传送带相切,倾斜滑道的倾角,滑道顶端高,该同学做了如下实验,将滑块由滑道顶端静止释放,同时将滑块沿传送带从顶端向下以初速度抛出,滑块和与传送带间的动摩擦因数均为,滑块与滑道之间的动摩擦因数,忽略两滑块的大小及在下端圆弧轨道上的运行时间,重力加速度,,,试求:
滑草是儿童非常喜欢的运动,简单的滑草赛道由斜坡道和水平道构成。其过程可简化为下图,其中滑板与斜坡道和水平道的动摩擦因数均相同,某次小明和姐姐去滑草,两人先后都从坡道上的点由静止下滑,在水平道上滑行一段距离后停止,姐姐的质量较大,坡道最低点处平滑连接,则下列说法正确的
如图所示,水平平台长为,平台端与长度为的由特殊材料制成的斜面平滑连接(物块通过端的速度大小不变,方向改变),斜面倾角为。在平台端放上质量为的物块,并给物块施加与水平方向成角的斜向下推力后,物块由静止开始运动。已知物块与平台间的动摩擦因数为,重力加速度,(下列计算结果可用分数、根号表示)
如图甲所示,游人半躺在滑草场专用的滑具里,从滑道的顶端由静止沿倾斜的滑道下滑,最后停在水平滑道上某一位置。图乙为整个滑道的简化示意图。设倾斜道的倾角为,高度为。滑具与倾斜滑道和水平滑道的动摩擦因数均为,重力加速度为,倾斜滑道和水平滑道平滑连接。下列说法正确的是
如图所示,一倾角为、足够长的斜面固定在水平地面上,斜面上放一质量为的小物块,小物块与斜面间的动摩擦因数,最大静摩擦力可认为等于滑动摩擦力,现用平行斜面向上的力推动小物块由静止开始运动(,,,最后的计算结果保留一位小数)。
可爱的企鹅喜欢在冰面上玩游戏。如图所示,有一企鹅在倾角为的倾斜冰面上,先以加速度从冰面底部由静止开始沿直线向上“奔跑”,时,突然卧倒以肚皮贴着冰面向前滑行,最后退滑到出发点,完成一次游戏(企鹅在滑动过程中姿势保持不变)。若企鹅肚皮与冰面间的动摩擦因数,,求:
今日推荐 ![]()
![]()
![]()
