高中 | 洛伦兹力 题目答案及解析
稿件来源:高途
高中 | 洛伦兹力题目答案及解析如下,仅供参考!
选修3-1
第三章 磁场
3.5 运动电荷在磁场中受到的力
洛伦兹力
有人设计了一粒种子收集装置。如图所示,比荷为$\dfrac{q}{m}$的带正电的粒子,由固定于$M$点的发射枪,以不同的速率射出后,沿射线$MN$方向运动,能收集各方向粒子的收集器固定在$MN$上方的$K$点,$O$在$MN$上,且$KO$垂直于$MN$。若打开磁场开关,空间将充满磁感应强度大小为$B$,方向垂直于纸面向里的匀强磁场,速率为$v_{0}$的粒子运动到$O$点时,打开磁场开关,该粒子全被收集,不计粒子重力,忽略磁场突变的影响。
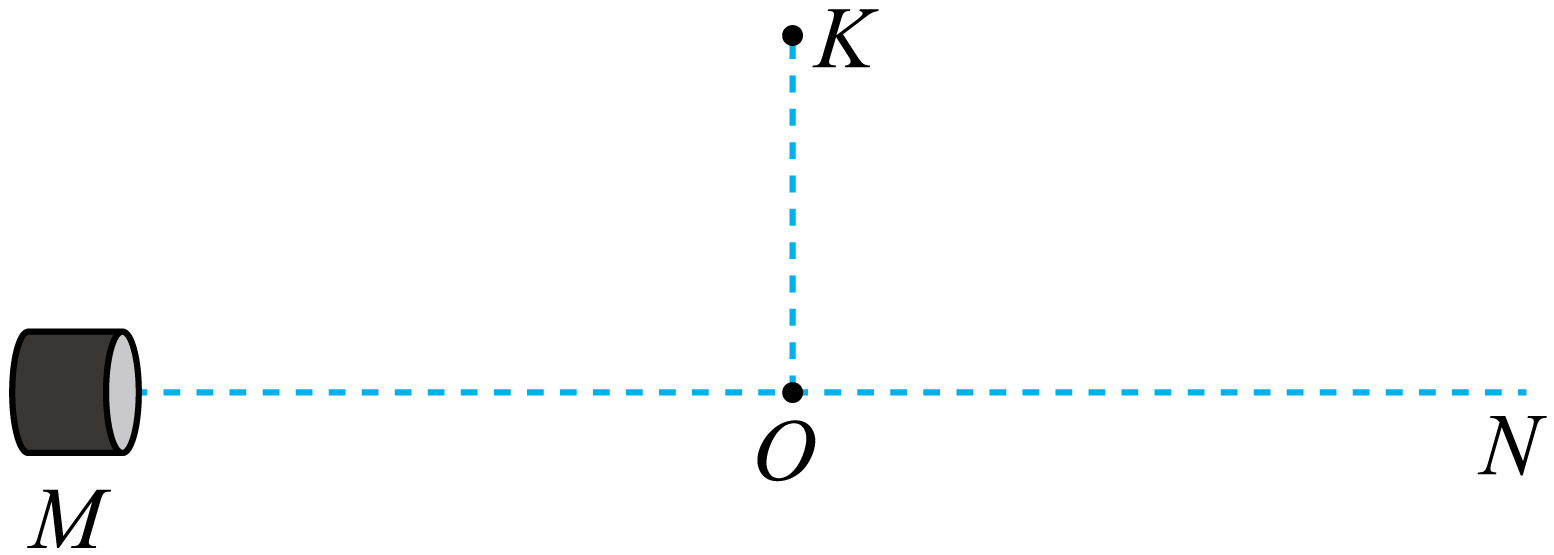
求$OK$间的距离;
$\\dfrac{2mv_{0}}{qB}$
"]]当粒子到达О点时打开磁场开关,粒子做匀速圆周运动,设轨迹半径为$r_{1}$,如图所示
由洛伦兹力提供向心力得$qv_{0}B=m\dfrac{v_{0}^{2}}{r_{1}}$
其中$OK=2r_{1}=\dfrac{2mv_{0}}{qB}$
速率为$4v_{0}$的粒子射出瞬间打开磁场开关,该粒子仍被收集,求$MO$间的距离;
$\\dfrac{2\\sqrt{3}mv_{0}}{qB}$
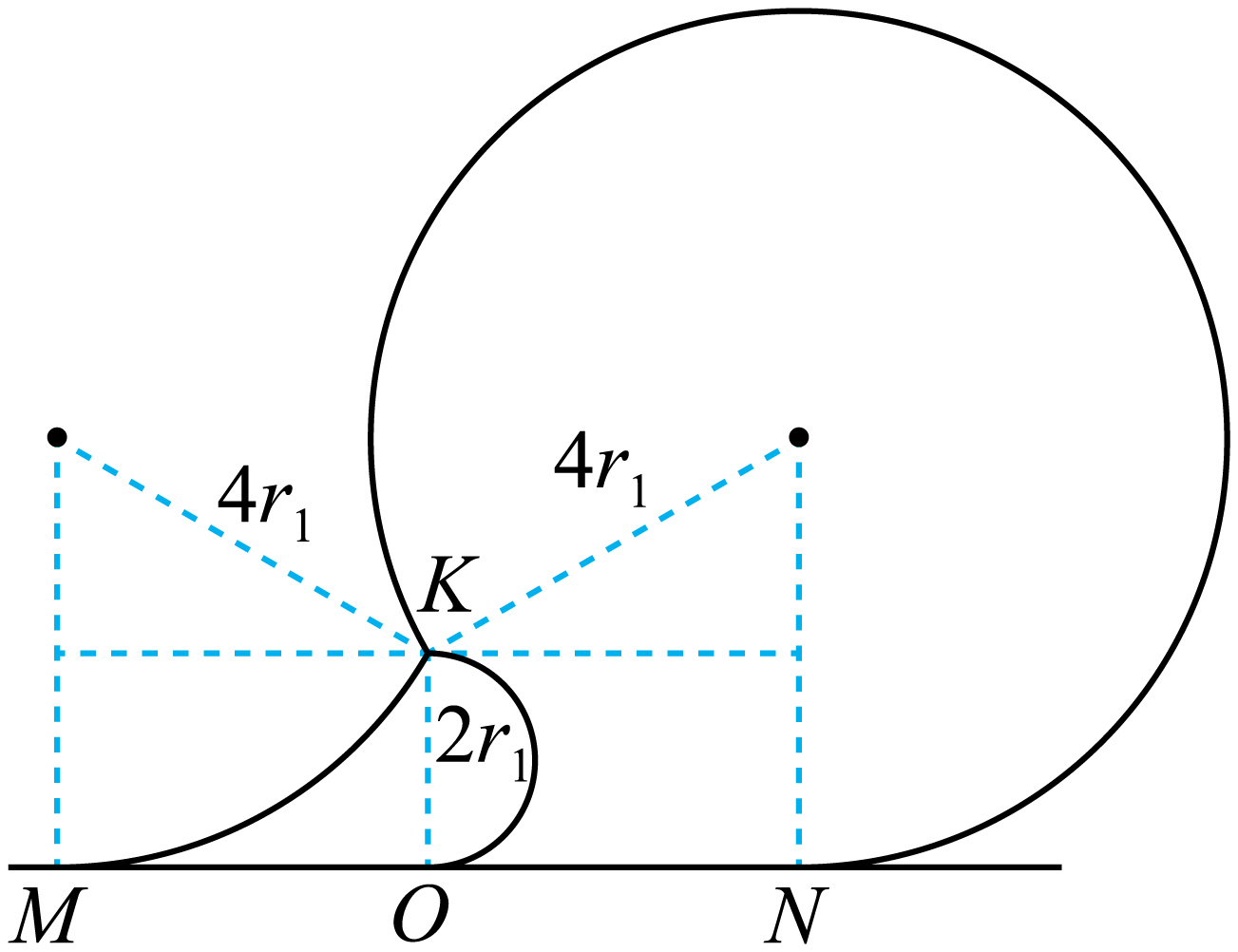
"]]速率为$4v_{0}$的粒子射出瞬间打开磁场开关,则粒子在磁场中运动的轨迹半径$r_{2}=4r_{1}$
如图所示,由几何关系有$(4r_{1}-2r_{1})^{2}+MO^{2}=(4r_{1})^{2}$
解得$MO=2\sqrt{3}r_{1}=\dfrac{2\sqrt{3}mv_{0}}{qB}$
速率为$4v_{0}$的粒子射出后,运动一段时间再打开磁场开关,该粒子也能被收集。以粒子射出的时刻为计时$O$点。求打开磁场的那一时刻。
$\\dfrac{\\sqrt{3}m}{qB}$
"]]速率为$4v_{0}$的粒子射出一段时间$t$到达$N$点,要使粒子仍然经过$K$点,则$N$点在$O$点右侧,如图所示

由几何关系有$(4r_{1}-2r_{1})^{2}+ON^{2}=(4r_{1})^{2}$
解得$ON=2\sqrt{3}r_{1}=\dfrac{2\sqrt{3}mv_{0}}{qB}$
粒子在打开磁场开关前运动时间为$t=\dfrac{MO+NO}{4v_{0}}$
解得$t=\dfrac{\sqrt{3}m}{qB}$
高中 | 洛伦兹力题目答案及解析(完整版)
