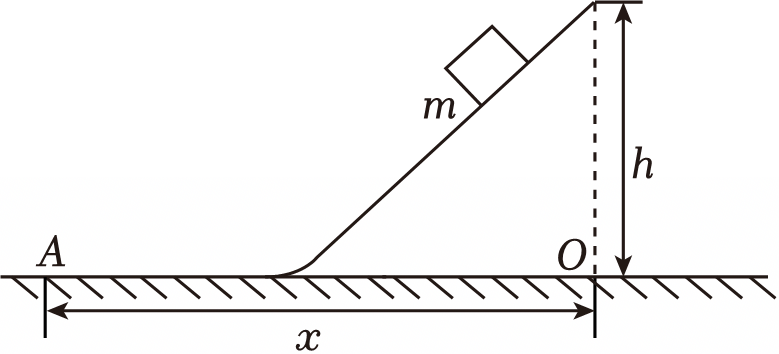
某一斜面固定在水平地面上，顶端到正下方水平面$O$点的高度为$h$，斜面与水平面平滑连接，斜面的倾角为$\theta$。一小木块从斜面的顶端由静止开始下滑，滑到水平面上的$A$点停下，已知木块与斜面、水平面间的动摩擦因数均为$\mu $，$A$点到$O$点的距离为$x$，重力加速度为$g$，则下列说法正确的是$(\qquad)$

整个过程摩擦力对小木块的功为$\\mu mgx$

只增加小木块的质量，其它条件不变，小木块停$A$点的右侧

只增加斜面的倾角，其它条件不变，小木块仍停在$A$点

在$A$点小木块获得$2mgh$大小的动能，小木块刚好滑到斜面顶端

$\rm A$、整个过程摩擦力对小木块的功为$W_{f}=-\mu mg\cos\theta\cdot \dfrac{h}{\sin\theta} -\mu mg\left(x- \dfrac{h}{\tan\theta}\right)=-\mu mgx$，故$A$错误；

$\rm BC$、从释放到停下的整个过程，根据动能定理得

$mgh-\mu mg\cos\theta\cdot \dfrac{h}{\sin\theta} -\mu mg\left(x- \dfrac{h}{\tan\theta}\right)=0$

可得$x=\dfrac{h}{\mu}$

可知小木块停下位置与小木块的质量和斜面的倾角均无关，所以只增加小木块的质量或只增加斜面的倾角，其它条件不变，小木块仍停在$\rm A$点，故$\rm B$错误，$\rm C$正确；

$\rm D$、若小木块在$A$点获得$2mgh$大小的动能，由于$E_{k0}=2mgh=mgh+\mu mgx$，可知小木块刚好滑到斜面顶端，故$\rm D$正确。

故选：$\rm CD$。