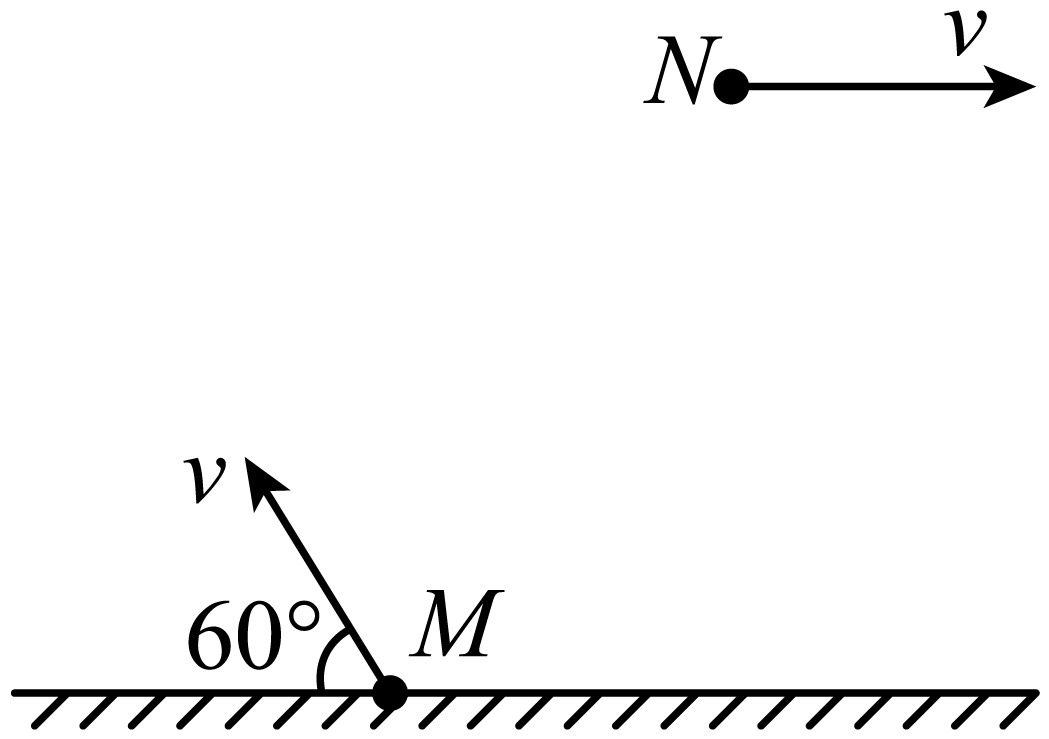
如图，竖直平面内有平行于该平面的匀强电场，一带电小球由$M$点斜向上抛出，速度大小为$v$、方向与水平面成$60^\circ $角，经过时间$t$到达$N$点，速度大小仍为$v$、方向水平向右。已知小球运动轨迹在该竖直平面内，重力加速度大小为$g$，$t=\dfrac{\sqrt{3}v}{g}$。下列说法正确的是$(\qquad)$

电场强度方向水平向右

小球受电场力大小为重力的$\\dfrac{1}{2}$

从$M$到$N$的过程，电场力做功为$\\dfrac{3}{4}mv^{2}$

从$M$到$N$的过程，小球的电势能先减少后增大

$\rm AB$．分析可知带电小球在电场中做匀变速曲线运动，以$M$点为坐标原点，水平向右为$x$轴正方向，竖直向上为$y$轴正方向，竖直方向的加速度$a_{y}=\dfrac{0-v\sin 60{^\circ}}{t}=- \dfrac{1}{2}g$

水平方向的加速度$a_{x}=\dfrac{v-(-v\cos 60{^\circ})}{t}=\dfrac{\sqrt{3}}{2}g$

设电场力为$F$，其水平方向的分力$F_{x}=ma_{x}=\dfrac{\sqrt{3}}{2}mg$

其竖直方向的分力为$F_{y}$，则$F_{y}-mg=ma_{y}$

得$F_{y}=\dfrac{1}{2}mg$

故电场力大小$F=\sqrt{F_{x}^{2}+F_{y}^{2}}=mg$，方向$\tan\theta=\dfrac{F_{y}}{F_{x}}=\dfrac{\dfrac{1}{2}mg}{\dfrac{\sqrt{3}}{2}mg}=\dfrac{\sqrt{3}}{3}$

得$\theta=30^\circ $，即电场力与$x$正方向成$30^\circ $斜向上，因小球带电性质未知，故不能判断电场强度方向，故$\rm AB$错误；

$\rm C$．从$M$到$N$的过程，竖直方向的高度$h=\dfrac{0-v_{y}^{2}}{2a_{y}}=\dfrac{3v^{2}}{4g}$，设电场力做功为$W$，由动能定理得$W-mgh=\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv^{2}$，解得$W=\dfrac{3}{4}mv^{2}$，故$\rm C$正确；

$\rm D$．由$\rm AB$选项分析可知，电场力与$x$正方向成$30^\circ $斜向上，$M$点电场力和速度方向垂直，从$M$到$N$的过程，电场力与速度方向为锐角，故电场力一直做正功，电势能减小，故$\rm D$错误。

故选：$\rm C$。