高中 | 牛顿第二定律的两类基本问题 题目答案及解析
稿件来源:高途
高中 | 牛顿第二定律的两类基本问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
牛顿第二定律的两类基本问题
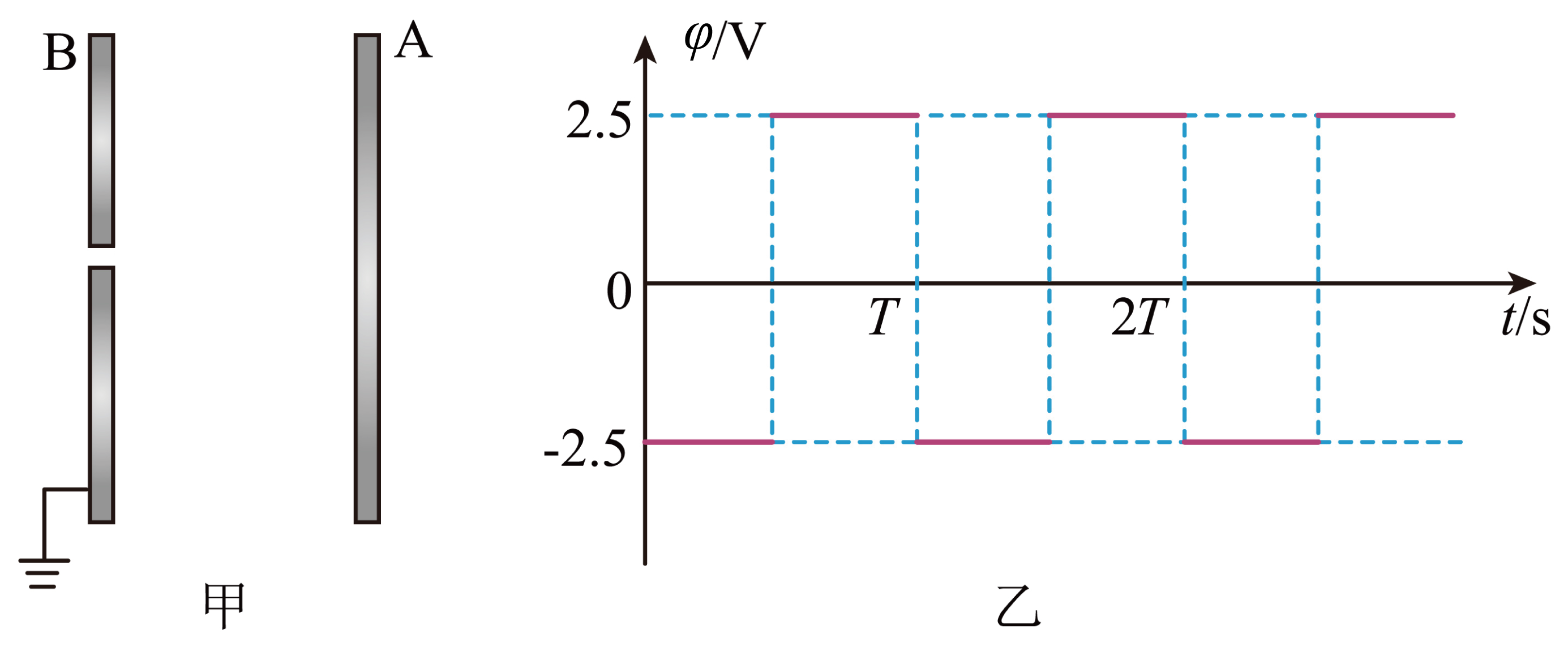
如图甲所示,真空中相距$d=10\;\rm cm$的两块平行金属板$A$、$B$与电源连接,$B$板接地,$A$板电势变化的规律如图乙所示。将一个质量为$m=2.0\times10^{-23}\;\rm kg$电荷量为$q=+1.6\times10^{-15}\;\rm C$的粒子在$t=\dfrac{T}{4}$时刻从紧临$B$板小孔处无初速度释放,粒子恰好不能到达$A$板,粒子重力不计。求:
粒子在平行板间运动时加速度的大小;
$a=2\\times10^{9}\\;\\rm m/s^{2}$
"]]平行金属板$A$、$B$间的电场强度$E=\dfrac{U}{d}$
由牛顿第二定律可知$qE=ma$
解得$a=2\times10^{9}\;\rm m/s^{2}$
$A$板电势变化的周期$T$。
$T=2\\sqrt{2}\\times10^{- 5}\\;\\rm \\text{s}$
"]]粒子在$t=\dfrac{1}{4}T$到$t= \dfrac{1}{2}T$时间内,向右做匀加速运动,在$t=\dfrac{1}{2}T$到$t= \dfrac{3}{4}T$时间内粒子向$A$板做匀减速运动;$t= \dfrac{3}{4}T$后反向运动,则粒子向右运动的最大位移$x=2 \times \dfrac{1}{2}a\left( \dfrac{T}{4} \right)^{2}=\dfrac{1}{16}aT^{2}$
粒子恰好不能到达$A$板$x=d$
解得$T=2\sqrt{2} \times 10^{- 5}\;\rm \text{s}$
高中 | 牛顿第二定律的两类基本问题题目答案及解析(完整版)
