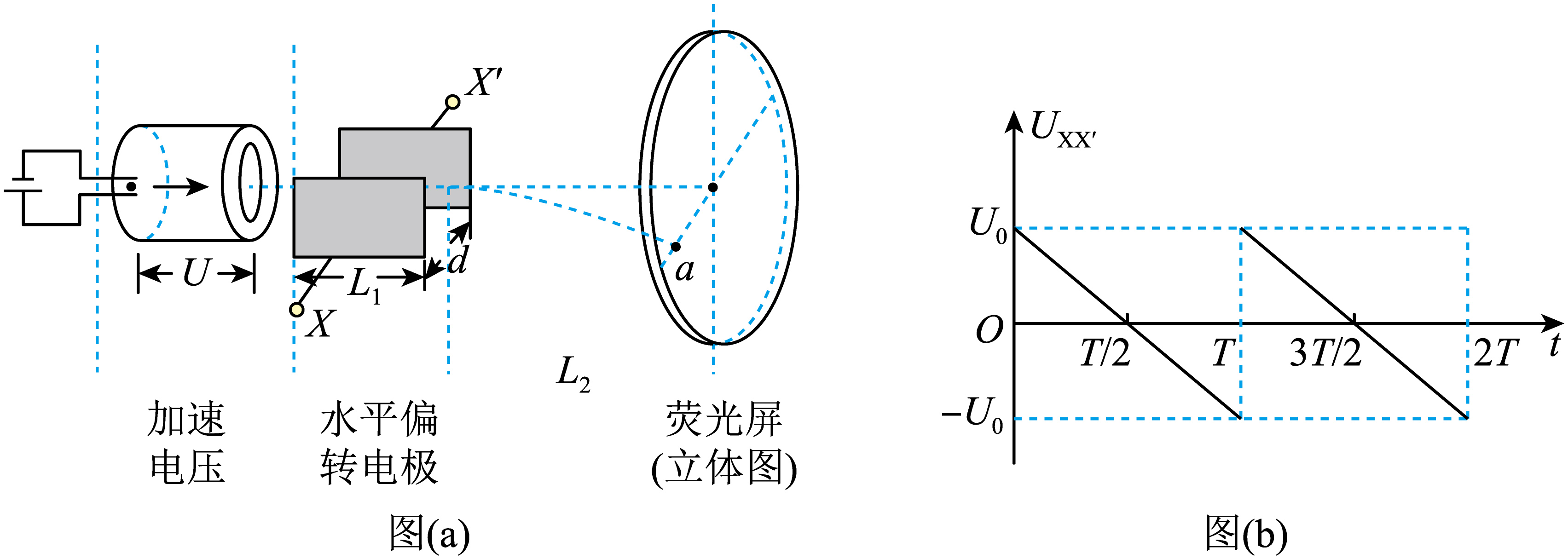
图（$a$）为示波管的部分原理图，电子经加速电压加速后，向右进入水平偏转电极，电极$X$、$X^\prime$间加上图（$b$）所示的扫描电压，内部可视为匀强电场（竖直偏转电极未画出）。已知加速电压为$U$，水平偏转电极长$L_{1}$，间距$d$，电极右端到荧光屏距离为$L_{2}$，当扫描电压周期为$T$，峰值为$U_{0}$时，荧光屏上可见一亮点在水平方向上移动。电子比荷为$\dfrac{e}{m}$，不计电子重力及电子间的相互作用力，电子通过水平偏转电极的时间极短。关于扫描过程，下列说法正确的是$(\qquad)$

电子射入偏转电极时的速度大小为$\\sqrt{\\dfrac{eU}{m}}$

$0\\sim $$\\dfrac{T}{2}$入射的电子有可能打到图（$a$）所示亮点$a$的位置

若要在荧光屏上看到一条水平亮线，应该降低扫描频率

荧光屏上亮点移动的速度为$\\dfrac{U_{0}L_{1}}{UdT}\\left(\\dfrac{L_{1}}{2}+L_{2}\\right)$

$\rm A$．电子在加速电场中，根据动能定理$eU=\dfrac{1}{2}mv_{0}^{2}$

可得，电子射入偏转电极时的速度$v_{0}=\sqrt{\dfrac{2eU}{m}}$

故$\rm A$错误。

$\rm B$．在$0-\dfrac{T}{2}$时间内，扫描电压为正，电子在水平偏转电极间受到沿$X^\prime X$的电场力，会向$X$侧偏转，所以$0-\dfrac{T}{2}$ 入射的电子有可能打到图（$a$）所示亮点$a$的位置，故$\rm B$正确。

$\rm C$．在荧光屏上看到一条水平亮线的条件需要减小扫描时间，即提高扫描频率，使得电子在荧光屏上的位置快速变化，由于视觉暂留效应，人眼就会看到一条连续的亮线，而不是降低扫描频率，故$\rm C$错误。

$\rm D$．电子在水平偏转电极间做类平抛运动，水平方向$L_{1}=v_{0}t_{1}$

竖直方向做匀加速直线运动，由牛顿第二定律有$e\dfrac{U_{0}}{d}=ma_{1}$

所以有$y_{1}=\dfrac{1}{2}a_{1}t_{1}^{2}=\dfrac{U_{0}L_{1}^{2}}{4Ud}$

离开偏转电场竖直方向速度为$v_{y}$，有$v_{y}=a_{1}t_{1}$

电子离开偏转电场，做匀速直线运动，水平方向位移$L_{2}=v_{0}t_{2}$

竖直方向有$y_{2}=v_{y}t_{2}=a_{1}t_{1}t_{2}=\dfrac{U_{0}e}{md} \times \dfrac{L_{1}}{v_{0}} \times \dfrac{L_{2}}{v_{0}}=\dfrac{U_{0}L_{1}L_{2}}{2Ud}$

则电子所打位置与$O$之间的距离为$Y=y_{1}+y_{2}=\dfrac{(L_{1}+2L_{2})L_{1}U_{0}}{4dU}$

由题图可知，其偏转电场$U$与时间在$0\sim T$内关系由题图结合数学知识可知为$U=\dfrac{2U_{0}}{T}t-U_{0}$

将其代入，整理有$Y=\dfrac{(L_{1}+2L_{2})L_{1}}{4dU}\left(\dfrac{2U_{0}}{T}t-U_{0}\right)$

由速度的定义可知，其是物体运动的位移与其时间的比值，在数学上的表示即为位移与时间函数的一阶导，可得荧光屏上亮斑移动的速度$v'=\dfrac{U_{0}L_{1}}{UdT}\left(\dfrac{L_{1}}{2}+L_{2}\right)$

故$\rm D$正确。

故选：$\rm BD$。